4.2 Color Space

4.2.1 CIE XYZ, xyY Color Spaces

Need for Standard Color Models

• Color is complex, with an infinite number of colors possible.
• Different devices and applications produce colors in different ways.
• A standard color model is necessary to:
  • Reproduce colors accurately.
  • Translate colors interchangeably between different devices and applications.
  • Represent each color numerically.
  • Identify the gamut (range) of all visible colors.

Contributions of Newton, Maxwell, and Grassmann

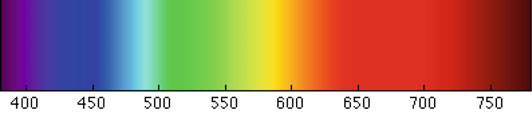
• Isaac Newton: Laid the foundation for understanding colors by splitting light into spectral colors (rainbow colors, Fig. 4.1). Showed that light is a mixture of pure colors, and object colors are due to reflectance of different wavelengths.
• James Clerk Maxwell: Discovered that mixing red, green, and blue monochromatic light could create other colors. Showed color mixing by projecting and superimposing three monochromatic pictures.
• Hermann Grassmann: Established that colors are additive. Formulated Grassmann’s Laws:
  • Any color can be matched by a linear combination of three primary colors (provided no primary can be matched by the other two).
  • A mixture of two colors can be matched by linearly adding their primary components.

CIE XYZ Color Space Based on Maxwell’s Tristimulus Theory and Trichromatic Vision

• Tristimulus Theory (Maxwell): Based on the trichromatic color vision theory of Young and Helmholtz.
• Trichromatic Color Vision (Young and Helmholtz): Human vision has three types of cones sensitive to three narrow bands of light (red, green, and blue).
• CIE (International Commission on Illumination): Developed the XYZ color space in 1931.

• Color Matching Functions:
  • Figure 4.2 shows the three color matching functions, indicating human eye response to visible colors.
  • 
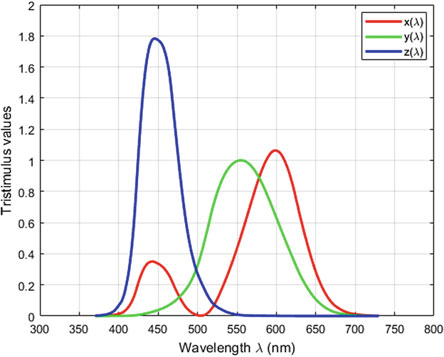
  • Peaks at approximately 600 nm (red), 550 nm (green), and 450 nm (blue).

• Primary Colors: CIE used three primary colors to match all spectral colors:
  • $R$: 700 nm (red)
  • $G$: 546.1 nm (green)
  • $B$: 435.8 nm (blue)
  • Chosen for practical reasons:
    • $G$ and $B$ were easily reproducible using mercury excitation lines.
    • 700 nm (R) has homogenous and nearly constant hue.

• Visible Light Spectrum and Tristimulus

  • Figure 4.1 represents visible light spectrum and the tristimulus.
  • 

• Color Matching and Representation:

  • Three primary stimuli are projected and mixed in various proportions to match spectral colors.

  • Each color represented as a three-value tuple: $(R,G,B)$.

  • Normalization to remove intensity:

    $r=\frac{R}{R+G+B}$ $g=\frac{G}{R+G+B}$ $b=\frac{B}{R+G+B}$

  (4.1)

  • $r$, $g$, $b$ are purely chromatic values.
  • Create three Color Matching Functions (CMF): $r(\lambda )$, $g(\lambda )$, $b(\lambda )$, where $\lambda$ is the wavelength.
  • CIE RGB color space is based on these three CMFs.

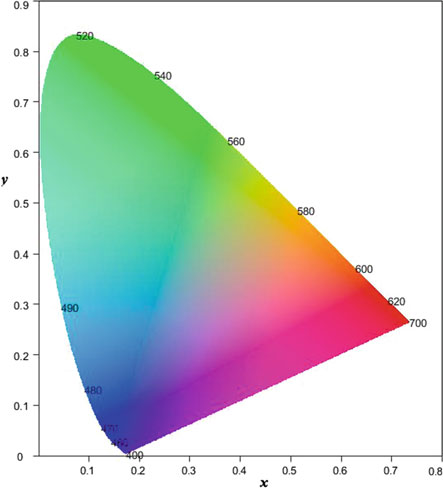
• CIE xy Chromaticity Diagram:

  • $r+g+b=1$, so $b$ is a dependent function ($b=1-r-g$).
  • Projecting the 3D $(r,g,b)$ curve onto the 2D $rg$ plane creates the horseshoe-shaped 2D $rg$ curve (cyan color in Fig. 4.3).
  • Transformation to CIE xy curve:
    • Align $g(\lambda )$ with the CIE luminosity function $V(\lambda )$.
    • Remove negative values in $r(\lambda )$.
  • CIE XYZ color space is based on the $xy$ curve.

• CIE xyY Color Space:

  • 
  • CIE $xy$ gamut only represents chromaticity (hue and saturation), not luminance (brightness).
  • Add luminance/brightness as the third dimension, $Y$.
  • CIE $xyY$ color space is the object color space:
    • $x$ and $y$ are chromaticity values.
    • $Y$ is the luminance value.

• Significance of CIE XYZ Color Space:
  • Provides a color gamut with all possible colors.
  • Specifies each color with a three-value tuple $(x,y,z)$.
  • Provides a reference for all other color models.
  • It is a device-independent color space.

4.2.2 RGB Color Space

• Device Dependence: RGB colors are device-dependent; different devices use different RGB primaries.

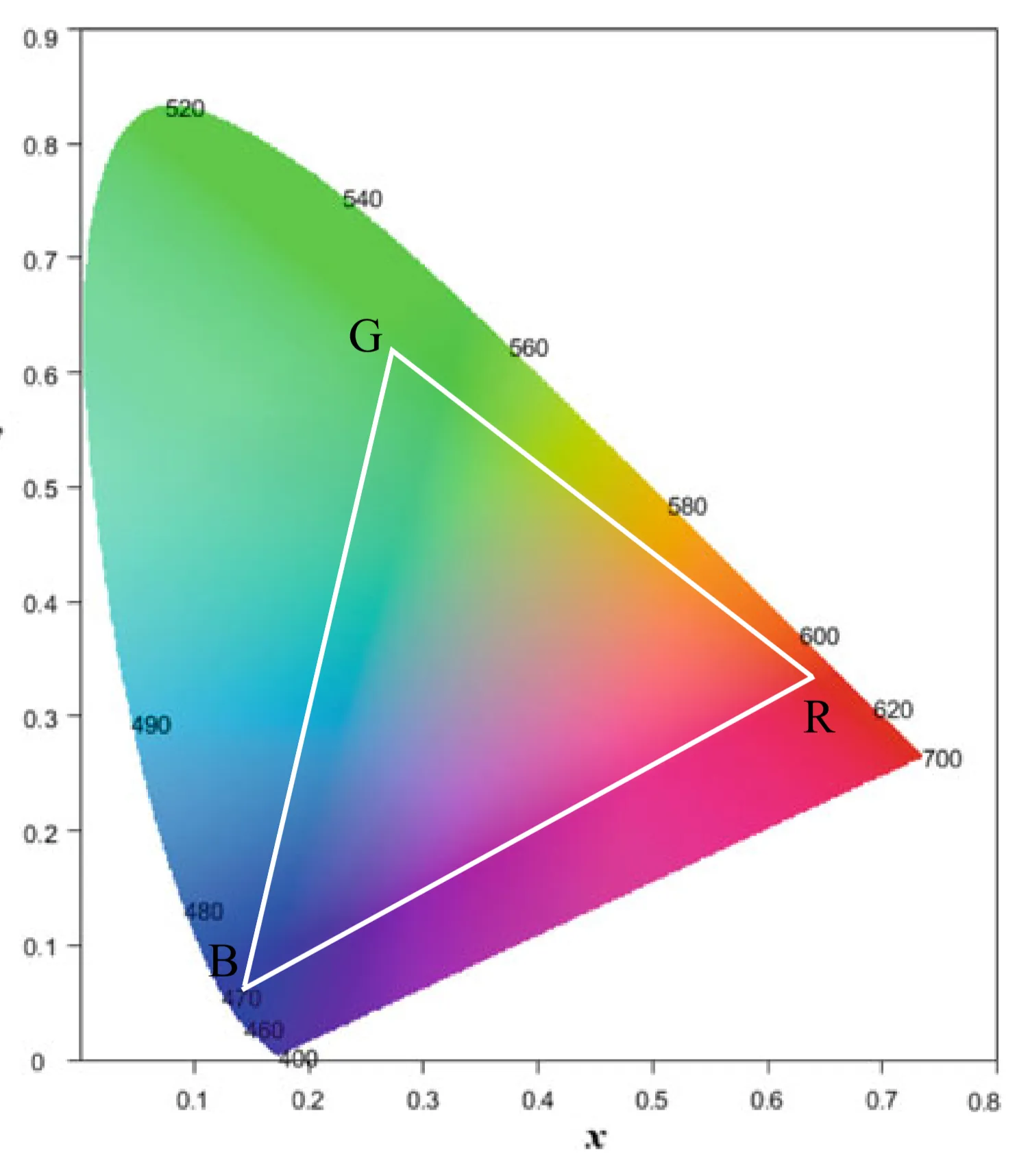
• sRGB: Computers use a standard RGB color model (sRGB).

  • sRGB primaries are chosen from the CIE XYZ color gamut.
  • sRGB gamut is a triangle inside the CIE XYZ gamut (Fig. 4.5).
  • 

• RGB Color Cube:

  • All possible colors created by the RGB palette can be visualized in a 3D cube (Fig. 4.6).

  • 

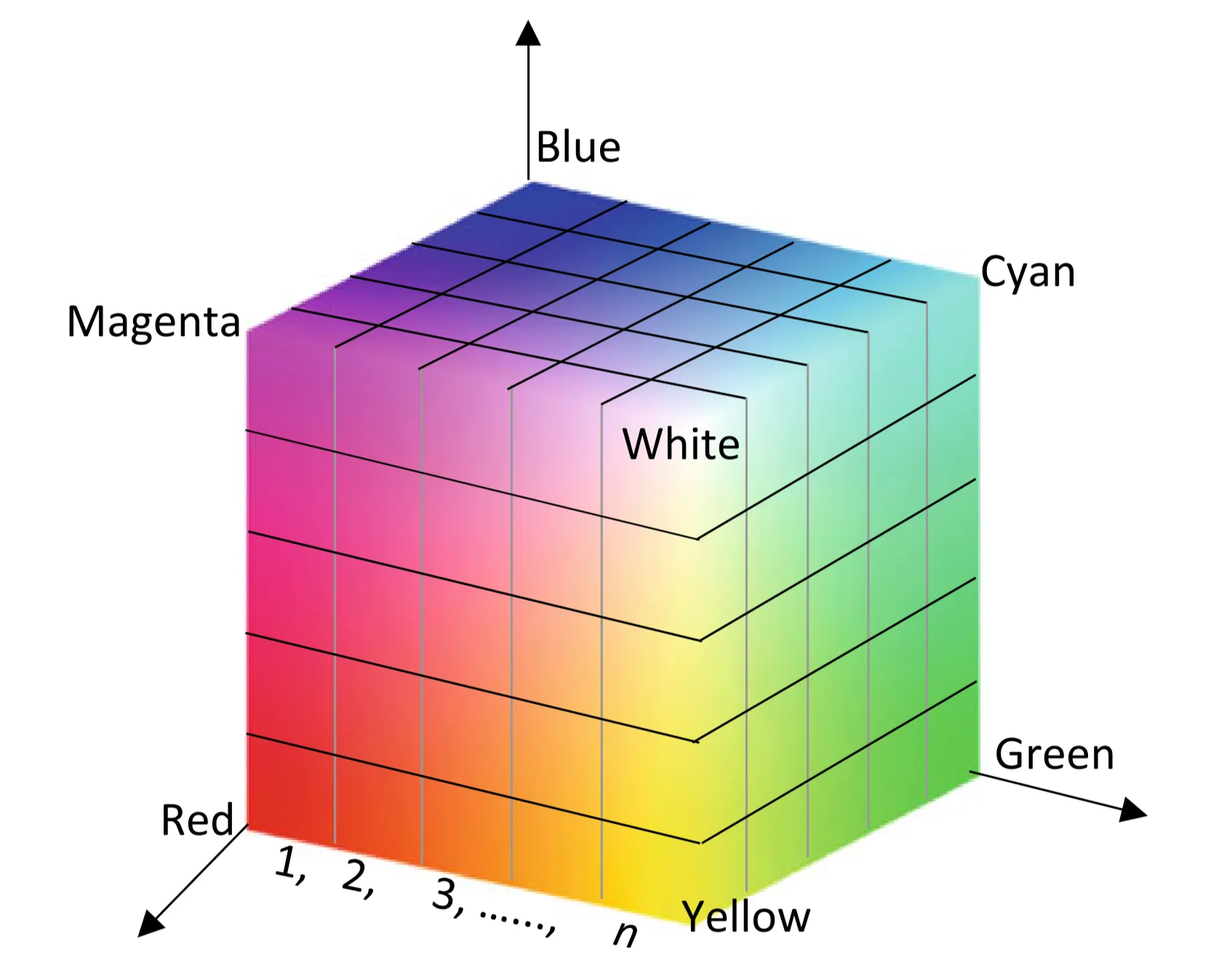
  • Colors are usually quantized.

  • Given pixel values $(r,g,b)$, a color $c$ is defined and reproduced as:

    $c=rR+gG+bB$

• Out-of-Gamut Colors:

  • RGB color spaces cannot represent all visible colors.
  • Approximation is needed for out-of-gamut colors.
  • For a color $C$ out of the RGB gamut, the approximation $C_A$ is the intersection of the RGB triangle and the line $CW$ (connecting $C$ and the white point $W$).
  • $C_A$ is a desaturated color of $C$.

4.2.3 HSV, HSL and HSI Color Spaces

• Deficiency of the RGB space:
  • RGB is not intuitive.
  • It does not conform to how humans perceive and make colors.
  • High correlation between three channels
• HSV and HSL definition
  • Intuitive because these are based on how artist make colors
  • H: Hue, S: Saturation, V: Value or B:Brightness, or L: Lightness

• Intuitive Color Mixing:

  • Artists use pigments (pure colors) and mix them with white, black, or gray.
  • Tints: Pure color + white (lighter colors).
  • Shades: Pure color + black (darker colors).
  • Tones: Pure color + gray (different purity/saturation).
  • Figure 4.7a illustrates tint, shades and tones using reddish colors.

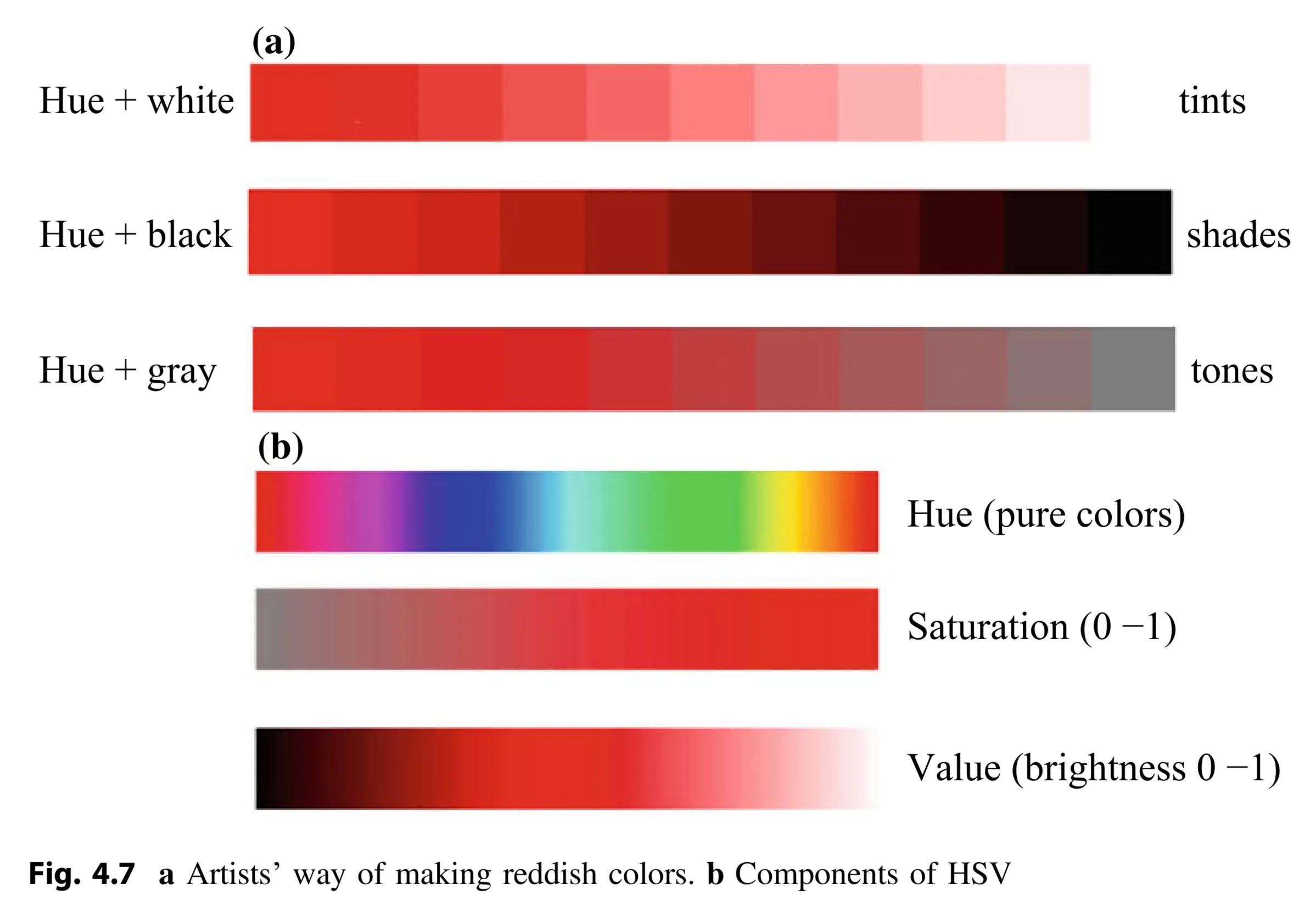
• HSV Color Model:

  • Based on how artists make colors.
  • Three components:
    • Hue (H): The pure color, determined by the dominant wavelength on the visible spectrum (Fig. 4.1).
    • Saturation (S): The colorfulness or vibrancy of the color. More saturated = more vivid.
    • Value (V) / Brightness: How bright or dark the color is.
  • Figure 4.7b illustrates the HSV color model with red.
  • Figure 4.8 Left: pure color on a ring, Right: hue-saturation wheel.
  • 

• HSV/HSL Cylinder, Cone, and Double Cone Representations:

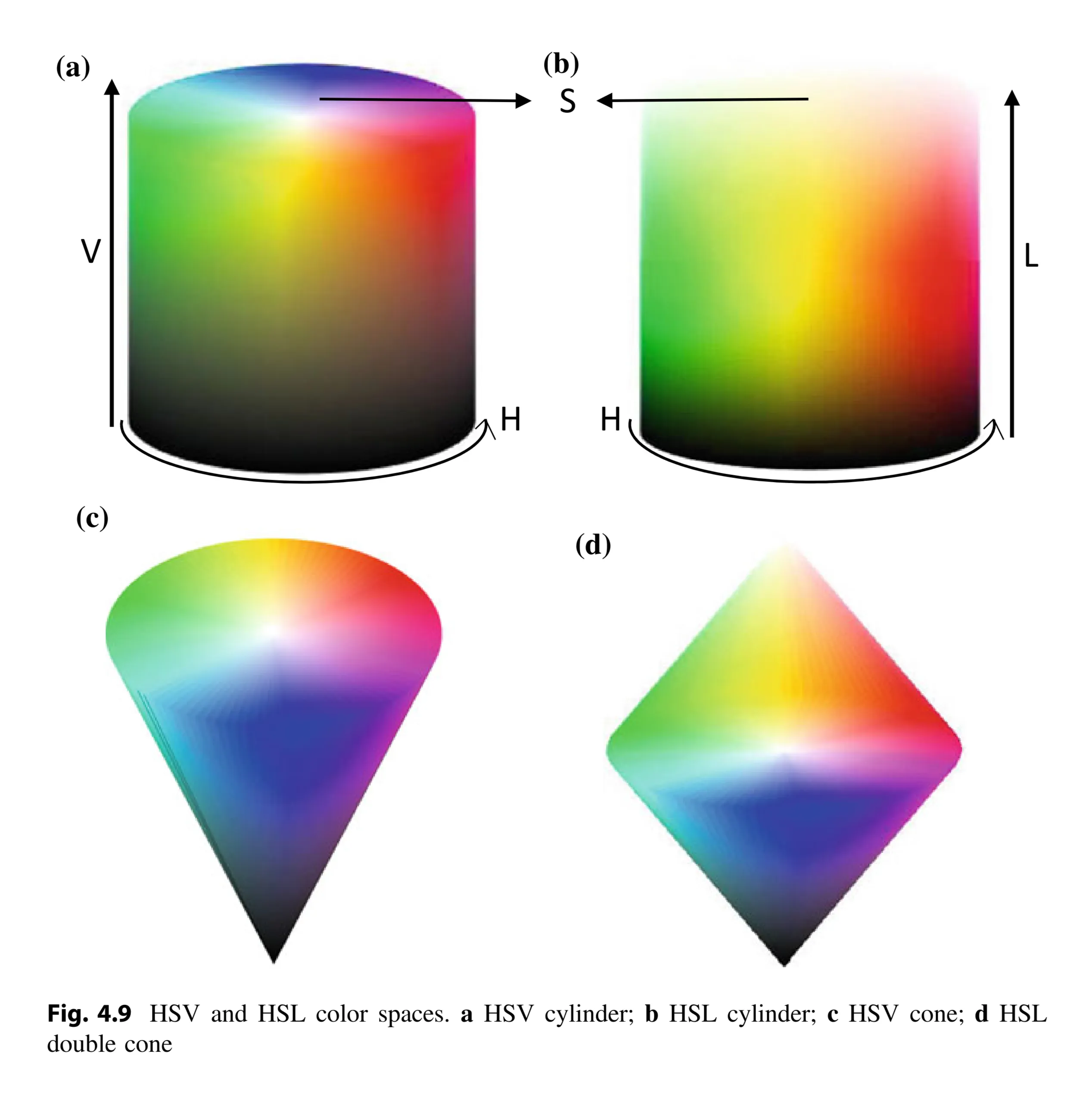
  • HSV Cylinder (Fig. 4.9a):
    • Pure colors (hues) are arranged in a circle.
    • Saturation varies along the radii of the circle, creating a hue-saturation disk.
    • Hue-saturation disks with different brightness are stacked to form a cylinder.
    • Most saturated colors are on the top (V = 1).
  • HSL Cylinder (Fig. 4.9b):
    • Similar to HSV, but the most saturated colors are in the middle.
    • The top of the cylinder is white (L = 1).
  • HSV Cone (Fig. 4.9c):
    • Colors become less colored (more redundant) as they go down the cylinder.
    • HSV is often represented as a single cone.
  • HSL Double Cone (Fig. 4.9d):
    • Colors become less colored as they go up or down the cylinder.
    • HSL is often represented as a double cone.
  • Radii of the cones are called “chroma” instead of “saturation.”

• Invariance to lighting variations.
  • The H and S are invariant to lighting variation or intensity changes.
  • It can be corrected by linear scaling

4.2.4 CIE LUV Color Space

• Non-Uniformity of CIE XYZ and RGB Spaces (MacAdam Ellipses):

  • CIE XYZ and RGB spaces are non-uniform in terms of color differences.
  • Calculated differences between colors are not proportional to perceived differences.
  • MacAdam ellipses (Fig. 4.11) illustrate this non-uniformity:
  • 
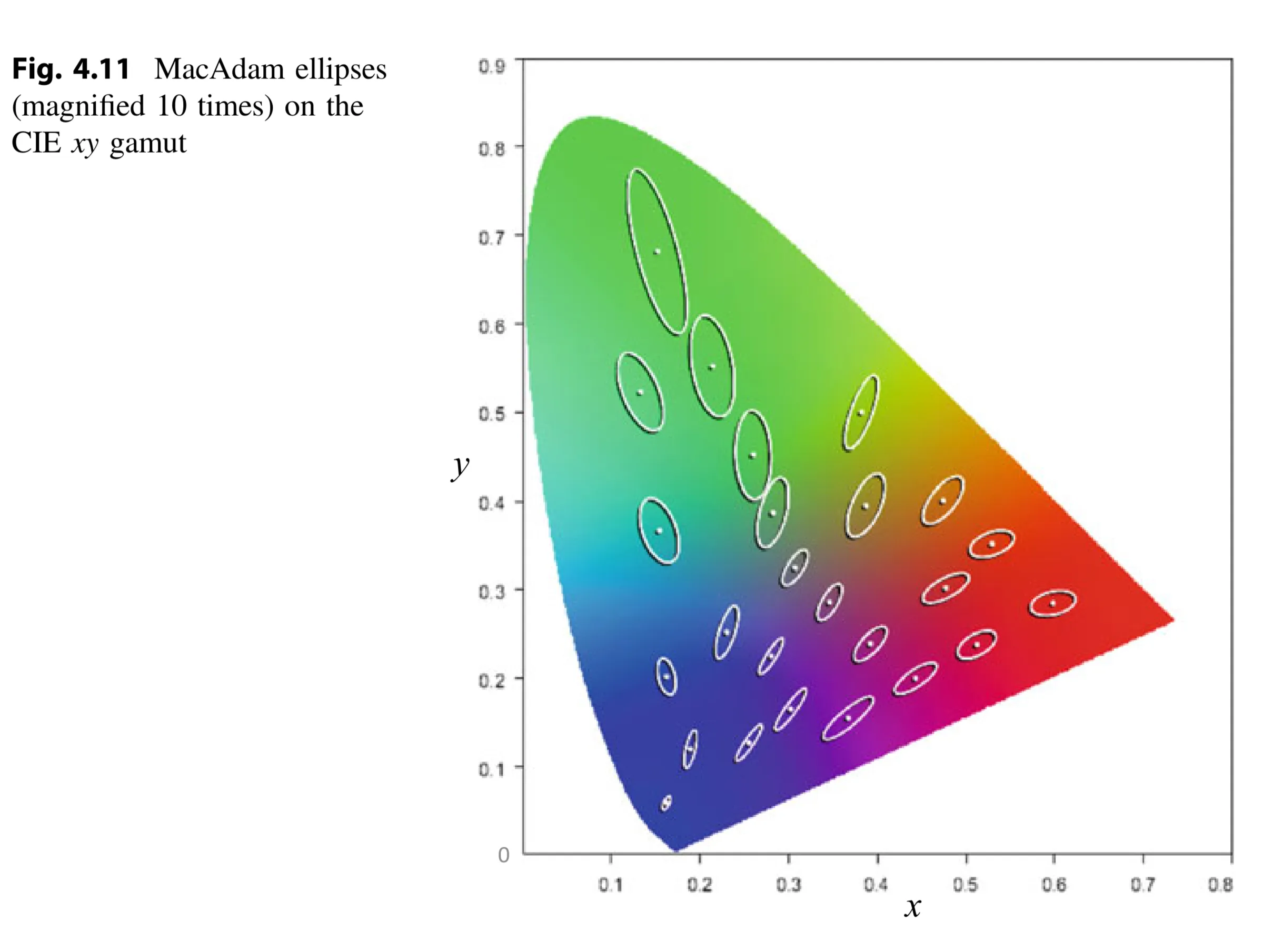
    • Each ellipse represents colors within the Just-Noticeable-Difference (JND) threshold.
    • Colors within an ellipse are perceivably the same.
    • Sizes of ellipses vary significantly across the gamut.

• CIE Luv and Lu’v’ Spaces to Address Non-Uniformity:

  • 
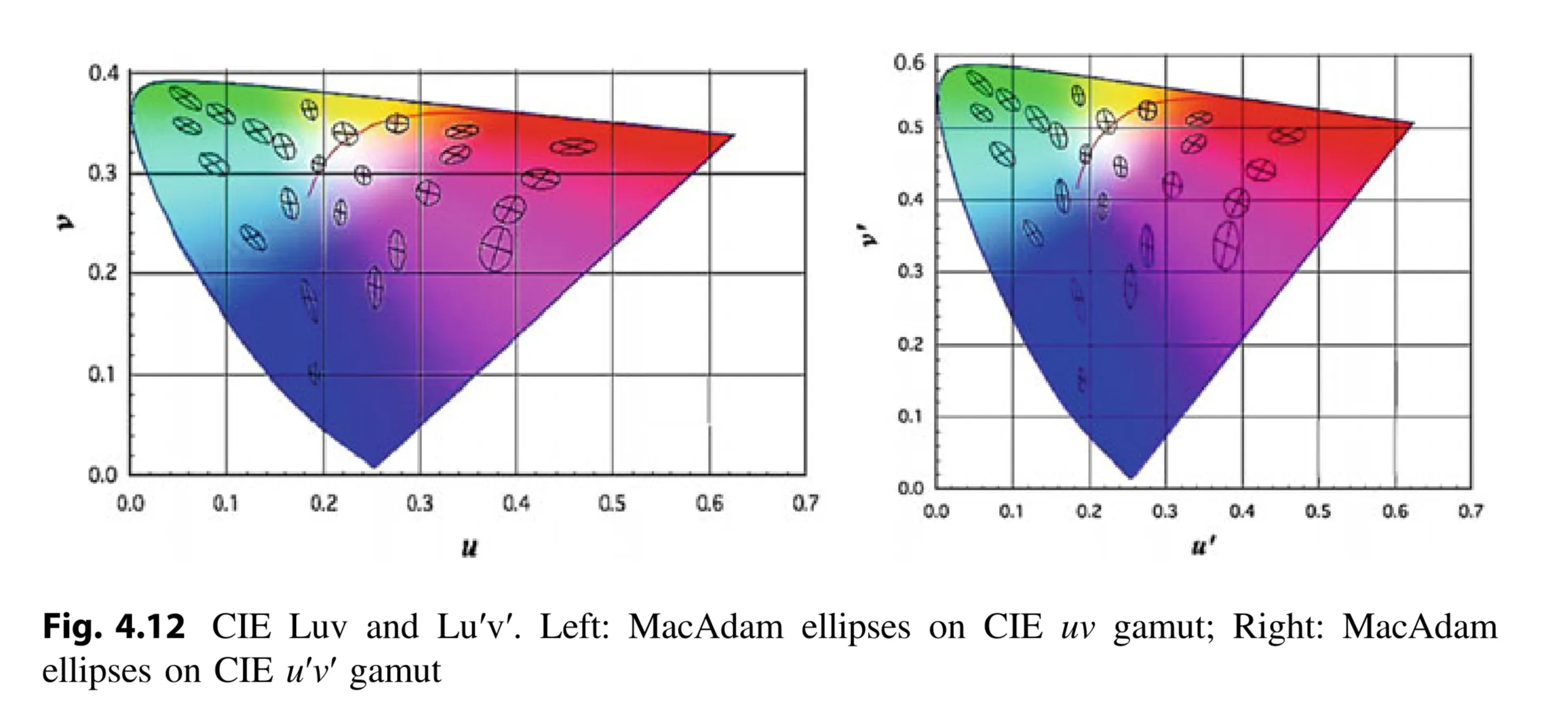
  • Created to overcome the non-uniform color spread problem.
  • Transformed from CIE XYZ space.
  • Idea: Stretch or squeeze the CIE $xy$ gamut to make MacAdam ellipses more uniform in size.

4.2.5 Y’CbCr Color Space

• Separation of Luminance and Chrominance:

  • Based on separating luminance from chromaticity (like HSV and LUV).
  • Ideal for many color applications, including image processing and feature extraction.

• Y’CbCr Transformation from RGB:

  $$\left[\begin{array}{c}{Y}^{\prime }\\ Cb\\ Cr\end{array}\right]=\left[\begin{array}{c}0\\ 128\\ 128\end{array}\right]+\left[\begin{array}{ccc}0.299& 0.587& 0.114\\ -0.169& -0.331& 0.500\\ 0.500& -0.419& -0.081\end{array}\right]\left[\begin{array}{c}R\\ G\\ B\end{array}\right]$$

  (4.21)

  • $Y^{\prime }$: Luminance.
  • $Cb$: Blue component.
  • $Cr$: Red component.
  • RGB and Y’CbCr values are in the range [0, 255].

• Advantages for Image Compression and Representation:

  • Most image information is concentrated in $Y^{\prime }$.
  • Channels can be treated independently (unlike RGB).
  • More importance can be given to $Y^{\prime }$.
  • More efficient communication (e.g., fewer bits for color channels) and more compact representation.
  • Example: Fig 4.13 shows an example of Y’CbCr channels
  • Y’ channel can be sent out independently