Harris Corner Detector

[Forstner and Gulch, 1987]

Searches for local neighborhoods where the image content has two main directions (eigenvectors of the autocorrelation matrix).

• Second Moment Autocorrelation Matrix:

$C(x,\sigma ,\tilde{\sigma })=G(x,\tilde{\sigma })\ast \left[\begin{array}{cc}{I}_x^2(x,\sigma )& I_x{I}_y(x,\sigma )\\ I_x{I}_y(x,\sigma )& I_y^2(x,\sigma )\end{array}\right]$

Where:

• $G(x,\tilde{\sigma })$ is a Gaussian kernel with standard deviation $\tilde{\sigma }$.

• $\tilde{\sigma }\approx 2\sigma$

• $I_x$ and $I_y$ represent the image gradients in the x and y directions, respectively.

• $\ast$ denotes convolution.

• The Gaussian kernel sums over all the pixels in a circular local neighborhood, weighting them according to a Gaussian distribution.

The autocorrelation matrix, C, can be decomposed and represented as:

$C=\left[\begin{array}{cc}\sum I_x^2& \sum I_x{I}_y\\ \sum I_x{I}_y& \sum I_y^2\end{array}\right]=R^{-1}\left[\begin{array}{cc}{\lambda }_1& 0\\ 0& {\lambda }_2\end{array}\right]R$

Where:

• ${\lambda }_1$ and ${\lambda }_2$ are the eigenvalues of C.

• R is a rotation matrix.

• The summation happens on neighborhood of x.

• Corner Condition: If ${\lambda }_1$ or ${\lambda }_2$ is about 0, the point is not a corner.

Harris Corner: Eigen Decomposition Visualization

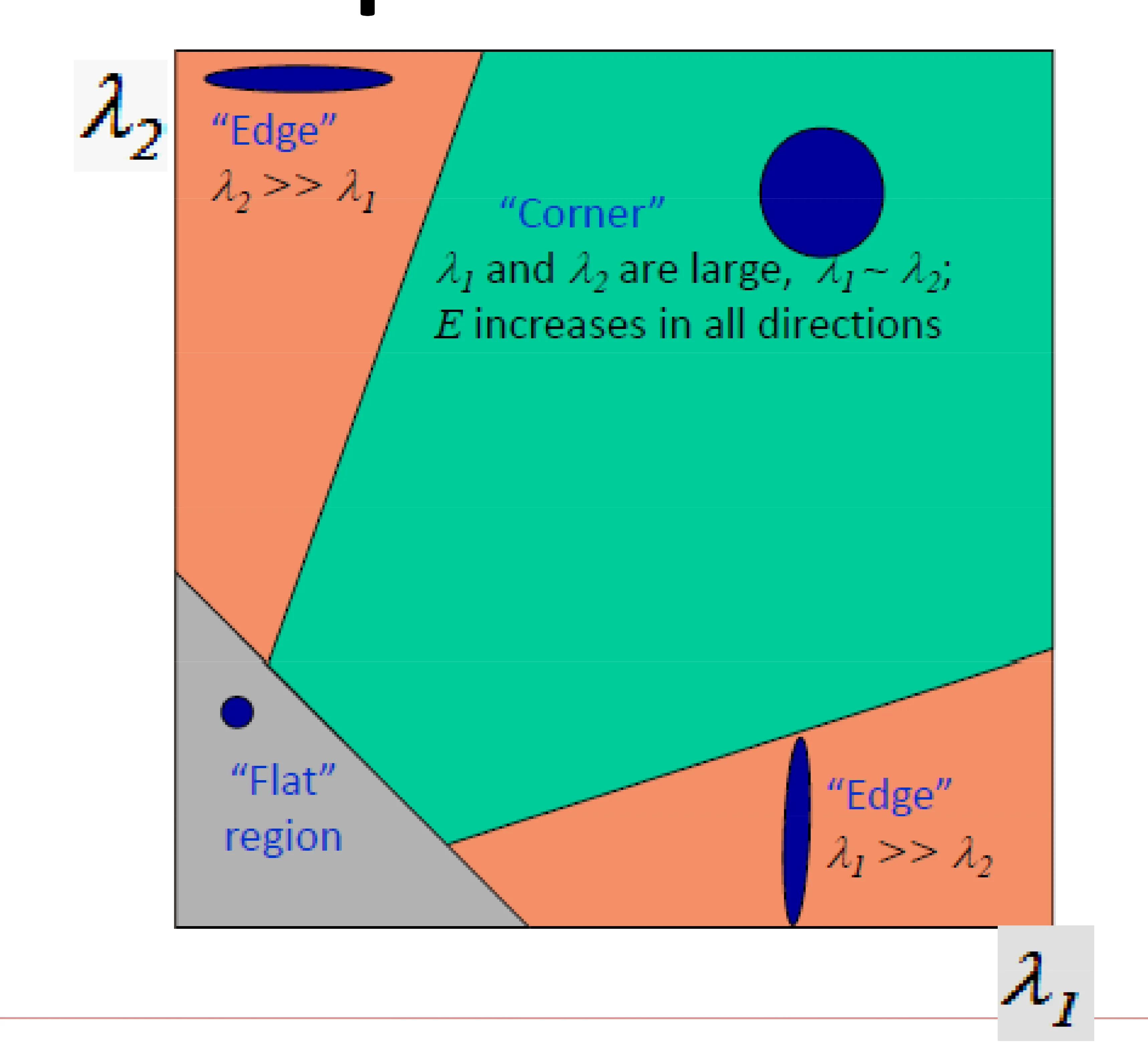
Feature_Detectors_and_Descriptors_old, p.10

• Edge: One eigenvalue is much larger than the other (${\lambda }_2>>{\lambda }_1$ or ${\lambda }_1>>{\lambda }_2$).
• Corner: Both eigenvalues are large, and ${\lambda }_1\sim {\lambda }_2$. The change in intensity (E) increases in all directions.
• Flat Region: Both eigenvalues are small.

Harris Corner: Different Approach

Instead of explicitly computing the eigenvalues, the following equivalence is used:

$\text{det}(C)={\lambda }_1{\lambda }_2$

$\text{trace}(C)={\lambda }_1+{\lambda }_2$

If $r=\frac{{\lambda }_1}{{\lambda }_2}(\ge 1)$, then $\frac{{\text{trace}}^2(C)}{\text{det}(C)}=\frac{({\lambda }_1+{\lambda }_2{)}^2}{{\lambda }_1{\lambda }_2}=\frac{(r{\lambda }_2+{\lambda }_2{)}^2}{r{\lambda }_2^2}=\frac{(r+1{)}^2}{r}=r+2+(1/r)$

Define the Harris cornerness measure, $H_c$:

$H_c=\text{det}(C)-\alpha \cdot {\text{trace}}^2(C)>\text{threshold}$

• $\alpha$ is a sensitivity parameter, typically in the range 0.04 - 0.25 (experimentally verified).
• Consider points where the Harris measure is greater than threshold. Let, $r=2$, then ${\text{trc}}^2=dc\ast (4.5)$
• For edge: r>>1, say 5, $H_c=dc(1-7.2\ast 0.1)=0.3\ast dc$
• For r = 10: $H_c=dc(1-12.1\ast 0.05)=0.4\ast dc$
• For corners, r = 2: $H_c=dc(1-4.5\ast 0.1)=dc\ast 0.55$

Harris Corner: Example

1. Image Derivatives: Compute the image derivatives $I_x$ and $I_y$.
2. Square of Derivatives: Calculate the squared derivatives: $I_x^2$, $I_y^2$, and $I_x{I}_y$.
3. Gaussian Filter: Apply a Gaussian filter $G({\sigma }_I)$ to the squared derivatives: $g(I_x^2)$, $g(I_y^2)$, and $g(I_x{I}_y)$.
4. Cornerness Function: Compute the Harris cornerness function $g(I_x{I}_y)$, where both eigenvalues are strong.

Harris Corner: Result

Effect: A very precise corner detector.