Support Vector Machines (SVMs) - Exam Preparation Notes
I. Introduction & Overview
- Q (Short): What is a Support Vector Machine (SVM), according to the definition provided? A: A system for efficiently training linear learning machines in kernel-induced feature spaces, while respecting the insights of generalization theory and exploiting optimization theory.
II. Basic Concepts
-
Q (Short): Write the formula for the scalar product of two vectors, and . A:
-
Q (Short): What is the general form of a decision function, , for binary classification, and what are the resulting class labels ()? A: . - If , then . - If , then .
-
Q (Medium): Briefly describe the core idea behind how SVMs work. A: SVMs find the best separating hyperplane between classes according to a criterion (e.g., maximum margin). The training process is an optimization problem, and the training data is effectively reduced to a set of support vectors.
III. Key Concepts: Feature Spaces and Kernels
-
Q (Short): Why might we map data to a higher-dimensional feature space? A: To make the data linearly separable, even if it isn’t in the original input space.
-
Q (Medium): What is a kernel function, and what property must it satisfy? A: A kernel function, , implicitly maps data to a new feature space. It must be equivalent to an inner product in some feature space. Formally, .
-
Q (Short): Give three examples of common kernel functions. A:
- Linear:
- Polynomial:
- Gaussian:
IV. Linear Separators and Maximum Margin
-
Q (Medium): How can binary classification be viewed in terms of feature space? A: Binary classification is the task of separating classes in feature space using a hyperplane. The decision function is .
-
Q (Long): Given multiple possible linear separators, how does an SVM choose the “optimal” one? Explain the concept of the margin. A: The SVM aims to find the hyperplane that maximizes the margin. The margin is the distance between the hyperplane and the closest data points from either class (the support vectors). A larger margin generally leads to better generalization.
-
Q (Medium): Explain the process of finding the optimal linear separator using convex hulls. A:
- Find the closest points in the convex hulls of the two classes.
- The optimal hyperplane bisects the line segment connecting these two closest points. The normal vector of the hyperplane, , is given by , where and are the closest points. The hyperplane equation is .
 [[SVMIITD.pdf#page=18&rect=191,23,529,315|]]
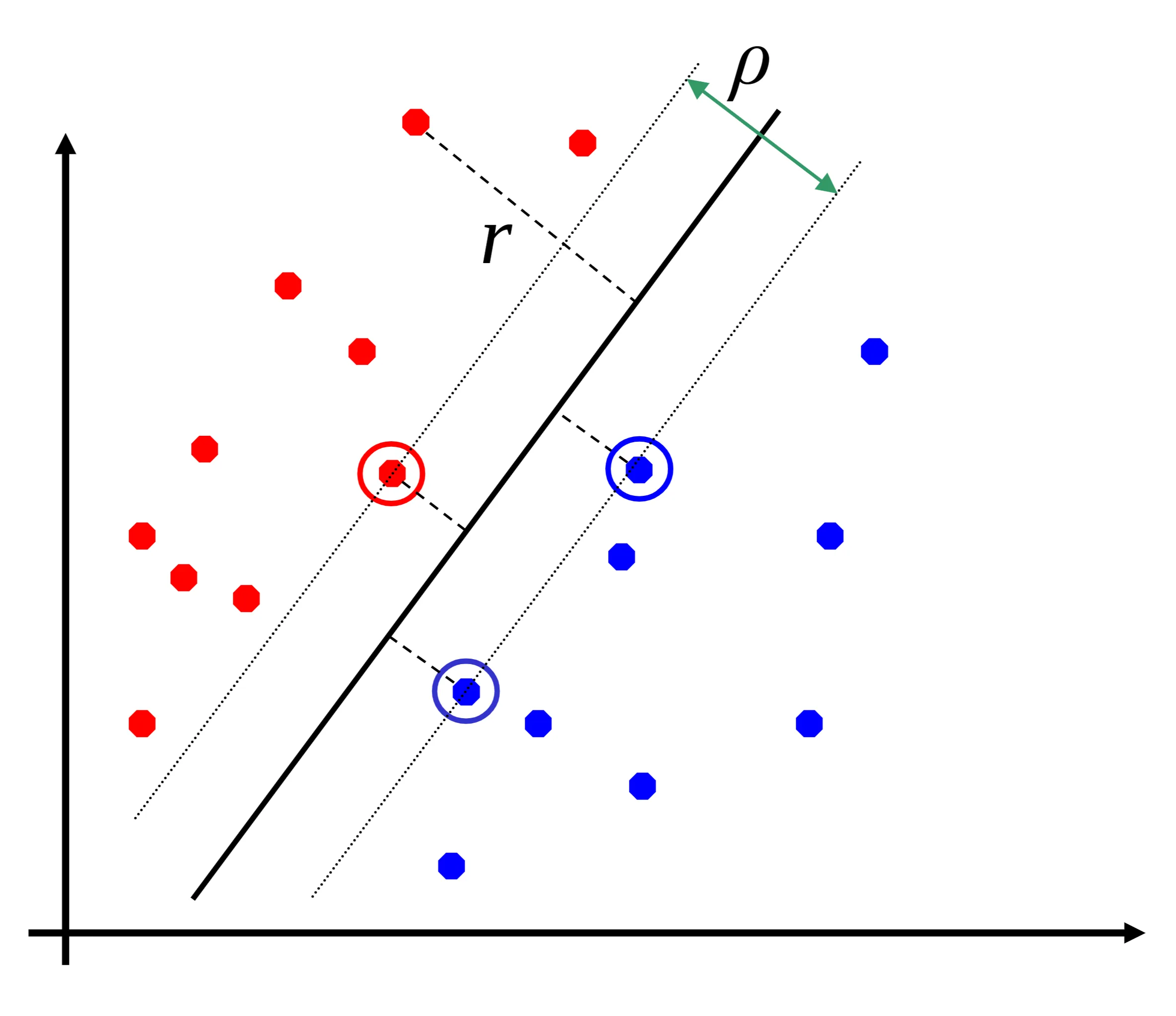
15. Q (Short): What are support vectors?
A: The data points closest to the separating hyperplane.
[[SVMIITD.pdf#page=18&rect=191,23,529,315|]]
15. Q (Short): What are support vectors?
A: The data points closest to the separating hyperplane.
-
Q (Short): What is the distance, , from an example data point to the separating hyperplane? A:
-
Q (Short): What is the margin, , of the separator? A is the width of separation between classes.
-
Q (Medium): Why is maximizing the margin considered a good strategy, both intuitively and theoretically? A:
- Intuitively: A larger margin provides more “buffer” against misclassification of new, unseen data.
- Theoretically: Maximizing the margin minimizes the complexity of the model (related to VC dimension), which helps prevent overfitting and improves generalization.
-
Q (Short): In maximum margin classification, which training examples are crucial, and which can be ignored? A: Only the support vectors are important; other training examples are ignorable.
V. Linear SVM - Mathematical Formulation
-
Q (Long): Formulate the optimization problem for finding the maximum margin hyperplane (the primal problem). Include the constraints. A: We want to find and such that:
- is maximized.
- Subject to the constraints:
- if
- if This is often reformulated as:
- Minimize:
- Subject to: for all .
-
Q (Long): Explain how the optimization problem is solved (the dual problem). What are Lagrange multipliers, and what is the final form of the solution? A: We use Lagrange multipliers, , one for each constraint. The dual problem is:
- Maximize:
- Subject to:
- for all The solution has the form:
- for any such that The classifying function is:
-
Q (Short): How do you identify support vectors from the solution of the dual problem? A: Support vectors correspond to training points where the Lagrange multiplier is non-zero.
-
Q(Medium): Explain the solution to the optimization problem. A: The solution is and for any such that . Each non-zero indicates that the corresponding is a support vector. The classifying function is .
VIII. Non-linear SVMs
-
Q (Medium): How do non-linear SVMs handle data that is not linearly separable? A: They map the data to a higher-dimensional feature space where the data becomes linearly separable (or nearly so, using a soft margin).
-
Q(Medium): Describe the non-linear classification with an example. A: Consider . Then, . Now consider , and we have,
-
Q (Long): Explain the “kernel trick.” Why is it important? A: The kernel trick avoids explicitly computing the mapping to the high-dimensional feature space, . Instead, we use a kernel function, , which computes the inner product in the feature space directly from the input space: . This is crucial because the feature space can be extremely high-dimensional (even infinite), making explicit computation infeasible.
-
Q (Long): How does the dual problem formulation change for non-linear SVMs? A: The only change is that the inner product is replaced by the kernel function :
- Maximize:
- Subject to:
- for all The classifying function becomes:
- Subject to:
- Maximize:
IX. Kernel Functions and Mercer’s Theorem
-
Q (Medium): What is a positive definite matrix? A: A square matrix A is positive definite if for all nonzero column vectors .
-
Q(Short): What is a negative definite, positive semi-definite and negative semi-definite matrix? A: A square matrix A is negative definite if for all nonzero column vectors . It’s positive semi-definite if , and negative semi-definite if .
-
Q (Medium): State Mercer’s theorem. Why is it important for SVMs? A: Mercer’s theorem states that every semi-positive definite symmetric function is a kernel. This is important because it provides a way to determine if a function is a valid kernel (i.e., corresponds to an inner product in some feature space) without having to explicitly find the feature mapping .
-
Q(Medium): What is a Gram Matrix? A: A matrix, K, composed of kernel values. For example:
-
Q (Short): Give examples of kernel functions besides the linear, polynomial, and Gaussian kernels. A: Two-layer perceptron:
X. SVM Applications and Extensions
-
Q (Short): List some application areas where SVMs have been successfully used. A: Text classification, genomic data analysis, and many other classification tasks.
-
Q (Short): Name two popular optimization algorithms for training SVMs. A: SMO (Sequential Minimal Optimization) and SVMlight.
-
Q (Medium): List some extensions to the basic SVM framework. A:
- Regression
- Variable Selection
- Boosting
- Density Estimation
- Unsupervised Learning (Novelty/Outlier Detection, Feature Detection, Clustering)