Hash Algorithms Short Notes

1. Hash Algorithm Working Procedure (General Structure)

• Core Component: Hash algorithms repeatedly use a compression function, denoted as $f$.
• Compression Function Inputs:
  • An $n$-bit input from the previous step, called the chaining variable ($CV$).
  • A $b$-bit block ($Y_i$) of the message being hashed.
• Compression Function Output: An $n$-bit output, which serves as the chaining variable for the next step.
• Initialization:
  • The chaining variable starts with an initial value ($IV$), specified by the algorithm. This is often denoted as $C{V}_0=IV$.
• Processing Blocks:
  • The input message $M$ is divided into $L$ blocks: $Y_0,Y_1,...,Y_{L-1}$, each of size $b$ bits.
  • The compression function is applied iteratively:
    • $C{V}_i=f(C{V}_{i-1},Y_{i-1})$ for $1\le i\le L$.
• Final Hash Value: The final output of the last compression step is the hash value (or message digest) of the entire message $M$.
  • $H(M)=C{V}_L$
• Diagram Description (Figure 11.8):
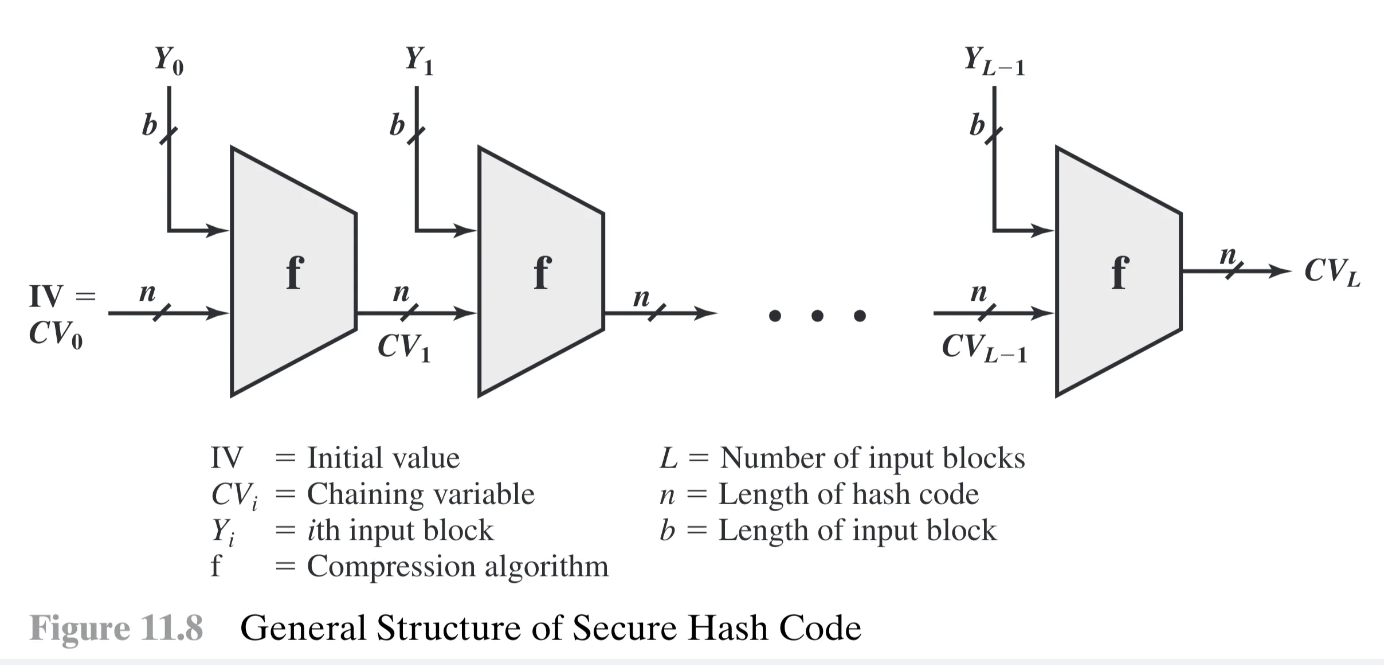
  • Shows a series of blocks representing the compression function $f$.
  • Each block takes the previous chaining variable ($C{V}_{i-1}$ of size $n$) and the current message block ($Y_{i-1}$ of size $b$) as input.
  • Each block produces the next chaining variable ($C{V}_i$ of size $n$).
  • Starts with $IV=C{V}_0$ and the first block $Y_0$.
  • Ends with the final hash $C{V}_L$ after processing the last block $Y_{L-1}$.
  • Key:
    • $IV$: Initial Value
    • $C{V}_i$: Chaining variable after step $i$
    • $Y_i$: $i^{th}$ input block (message block)
    • $f$: Compression algorithm
    • $L$: Number of input blocks
    • $n$: Length of hash code (and chaining variable)
    • $b$: Length of input block
• Note on Compression: Often, the block size $b$ is larger than the hash output size $n$, hence the term “compression”.

3. Motivation: Signing Long Messages

• Context: Digital signatures (e.g., RSA, discrete log-based) have limitations on the size of the message they can sign directly.
  • Example: RSA message length is limited by the modulus size (e.g., $1024$-$3072$ bits, or $128$-$384$ bytes).
  • Real-world messages (emails, files) are often much larger.
• Question: How to efficiently and securely compute signatures for large messages?
• Naive Approach (Similar to ECB mode in block ciphers):
  1. Divide the large message $x$ into smaller blocks $x_1,x_2,...,x_n$, each small enough for the signature algorithm.
  2. Sign each block $x_i$ separately using the private key $k_{pr}$ to get signatures $s_1,s_2,...,s_n$.
  • Diagram Description (Fig 11.1 - Insecure approach): Shows message blocks $x_1$ to $x_n$. Each block is independently fed into a “sig” box (signing algorithm) with the private key $k_{pr}$, producing individual signatures $s_1$ to $s_n$.
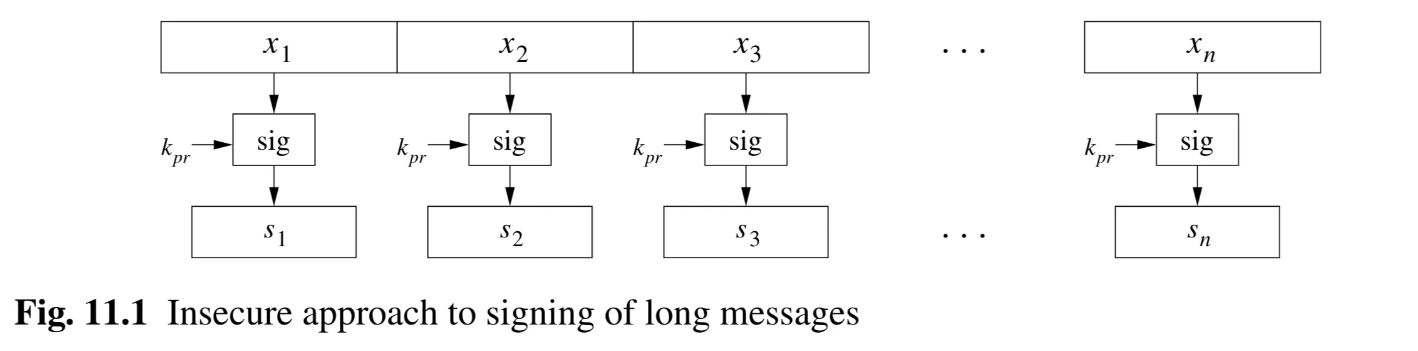
• Problems with the Naive Approach:
  • Problem 1: High Computational Load:
    • Asymmetric operations (like modular exponentiation in RSA) are computationally intensive.
    • Signing and verifying many small blocks takes significant time and energy, especially for large messages (email attachments, multimedia).
  • Problem 2: Message Overhead:
    • The total signature length is the same as the message length (or larger).
    • Example: A $1$ MB message yields a $1$ MB RSA signature, requiring $2$ MB total transmission.
  • Problem 3: Security Limitations (Most Serious):
    • Lack of protection for the whole message integrity.
    • Attacks Possible:
      • An attacker (Oscar) can remove blocks and their corresponding signatures.
      • Oscar can re-order blocks and their signatures.
      • Oscar can reassemble new messages from fragments of blocks and signatures from previous messages.
    • Manipulations within a block are prevented by the signature, but manipulations of the blocks are not.
• Desired Solution: One short signature for a message of arbitrary length.
• Solution using Hash Functions:
  1. Compute a short, fixed-size “fingerprint” (the hash value $h(x)$) of the entire message $x$ using a cryptographic hash function $h$.
  2. Sign only the hash value $h(x)$ using the private key $k_{pr}$ to get a single, short signature $s$.
  • Diagram Description (Fig 11.2 - Signing with hash function): Shows message blocks $x_1$ to $x_n$ being fed into a hash function $h$. The single output hash value is then fed into the “sig” box with the private key $k_{pr}$ to produce one signature $s$.

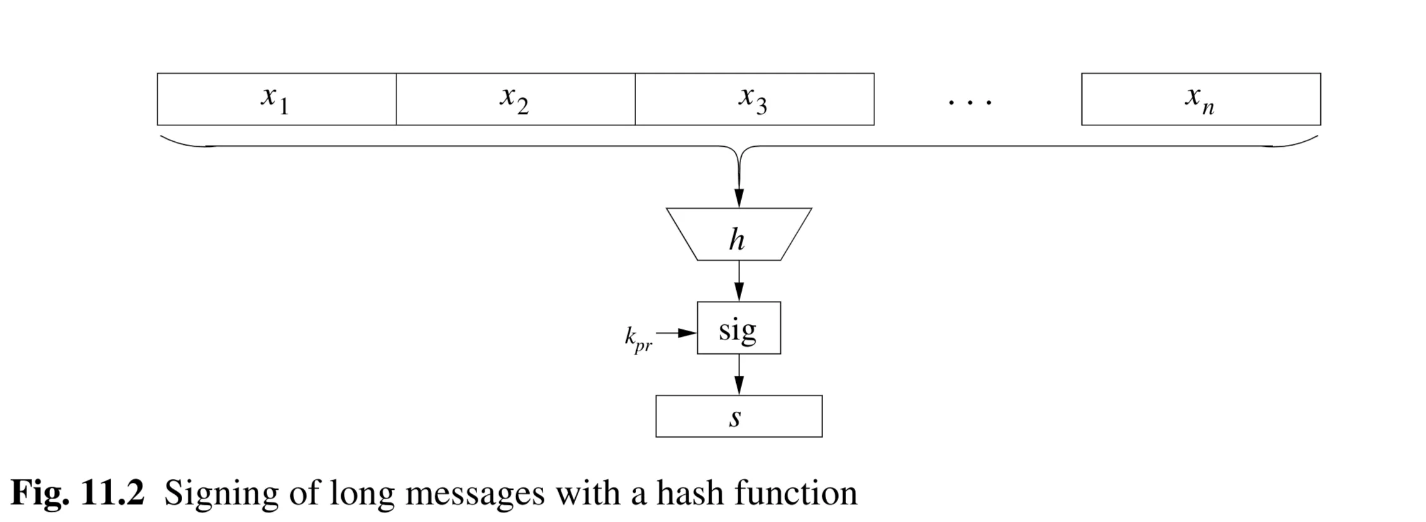
4. Security Requirements of Hash Functions

• Key Characteristic: Unlike other crypto algorithms, hash functions typically do not use keys.
• Need for Security: Despite not encrypting or using keys, weaknesses in hash functions can compromise the security of applications (like digital signatures).
• Three Central Security Properties:
  1. Preimage Resistance (One-Wayness)
  2. Second Preimage Resistance (Weak Collision Resistance)
  3. Collision Resistance (Strong Collision Resistance)
• Diagram Description (Fig 11.4 - Three security properties):

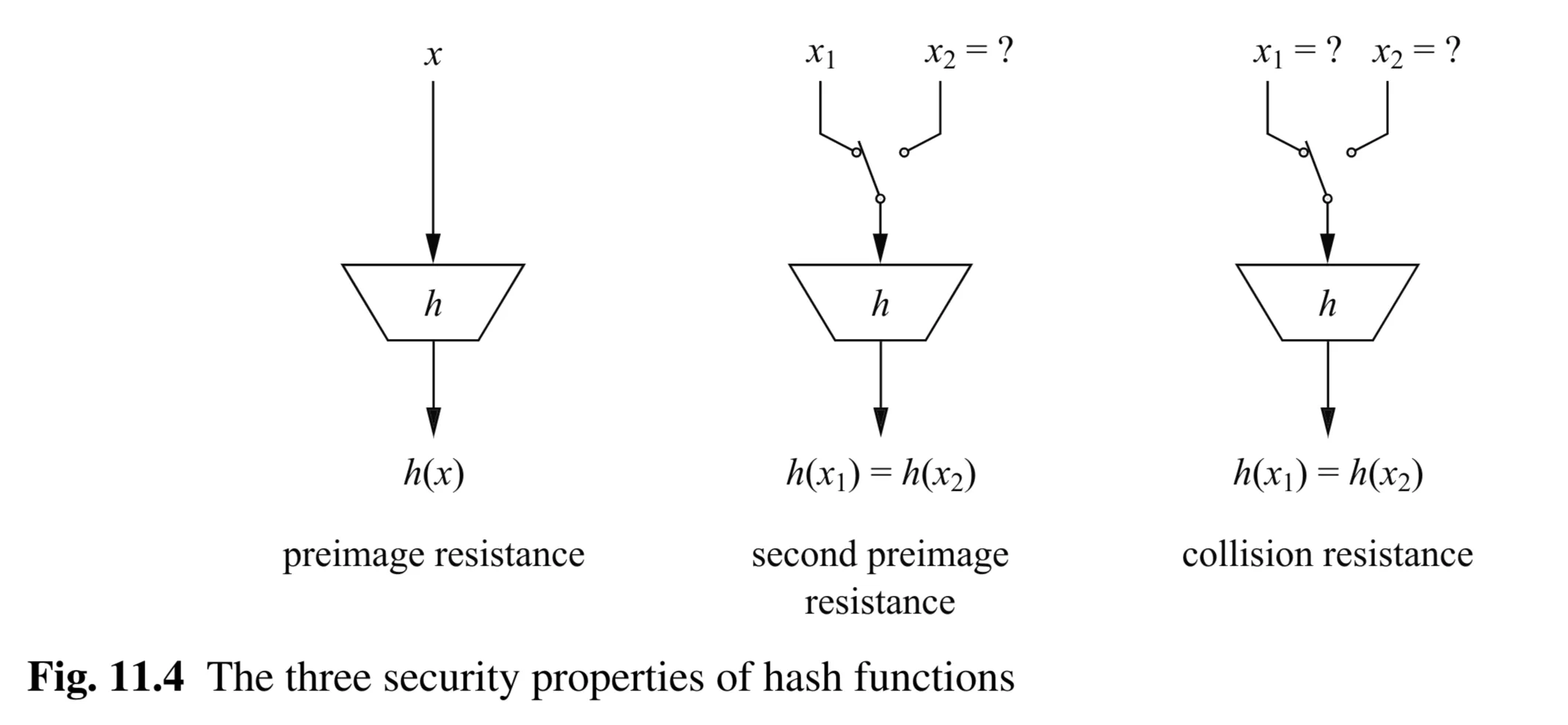
4.1 Preimage Resistance (One-Wayness)

• Definition: Given a hash output $z$, it must be computationally infeasible to find any input message $x$ such that $h(x)=z$.
• Analogy: Easy to compute $h(x)$ from $x$, but hard to compute $x$ from $h(x)$.
• Security Level: For an $n$-bit hash function, a brute-force attack requires trying, on average, $2^n$ inputs.

4.2 Second Preimage Resistance (Weak Collision Resistance)

• Definition: Given a specific input message $x_1$, it must be computationally infeasible to find a different input message $x_2$ (where $x_1\ne x_2$) such that $h(x_1)=h(x_2)$.
• Importance: Essential for digital signatures. If an attacker can find a second preimage $x_2$ for a signed message $x_1$, they could claim the signature for $x_1$ also applies to $x_2$.
• Security Level: For an $n$-bit hash function, a brute-force attack requires trying, on average, $2^n$ inputs $x_2$ to match the hash of the given $x_1$.

4.3 Collision Resistance (Strong Collision Resistance)

• Definition: It must be computationally infeasible to find any pair of distinct input messages $x_1,x_2$ (where $x_1\ne x_2$) such that $h(x_1)=h(x_2)$.
• Difference from Second Preimage: The attacker can choose both messages ($x_1$ and $x_2$), whereas for second preimage, $x_1$ is fixed. This makes finding collisions generally easier.
• Importance: Prevents attackers from creating two different messages (e.g., a legitimate contract and a fraudulent one) that have the same hash, then tricking someone into signing the hash corresponding to the legitimate one, while later claiming it applies to the fraudulent one.
• Attack Method: Often relies on the Birthday Attack.
• Security Level: Due to the Birthday Attack, finding a collision for an $n$-bit hash function requires approximately $2^{n/2}$ operations, significantly less than $2^n$.

4.4 Summary: Properties of Hash Functions (Page 5 List)

1. Arbitrary Message Size: Can be applied to messages $x$ of any size (though practical limits like SHA-512’s $2^{128}$ exist).
2. Fixed Output Length: Produces a hash value $z=h(x)$ of a fixed length $n$.
3. Efficiency: Computing $h(x)$ is relatively easy and fast.
4. Preimage Resistance: Given $z$, infeasible to find $x$ such that $h(x)=z$. (One-way).
5. Second Preimage Resistance: Given $x_1$, infeasible to find $x_2\ne x_1$ such that $h(x_1)=h(x_2)$. (Weak collision resistance).
6. Collision Resistance: Infeasible to find any pair $x_1\ne x_2$ such that $h(x_1)=h(x_2)$. (Strong collision resistance).

5. Collision Resistance and the Birthday Attack

• Pigeonhole Principle: Collisions must exist if the number of possible inputs is larger than the number of possible outputs. Hash functions map potentially infinite inputs to a fixed number ($2^n$) of outputs.
• Question: How hard is it to find a collision?
• Initial Guess: Might seem as hard as finding a second preimage (requiring $2^n$ operations for an $n$-bit` hash).
• Surprising Result: Finding a collision is much easier, requiring only about $2^{n/2}$ operations due to the Birthday Attack.

5.1 The Birthday Paradox (Analogy)

• Question: How many people are needed in a room so there’s a reasonable chance (e.g., 50%) that at least two share the same birthday? (Assume 365 days).
• Intuition: Might guess around $365/2\approx 183$ people.
• Actual Result: Far fewer people are needed.
• Calculating Probability of No Collision:
  • 1 Person: $P(\text{no collision})=1$
  • 2 People: The second person must have a different birthday than the first.
    • $P(\text{no collision among 2})=(1-\frac{1}{365})=\frac{364}{365}$
  • 3 People: The third person must have a different birthday than the first two.
    • $P(\text{no collision among 3})=(1-\frac{1}{365})\times (1-\frac{2}{365})=\frac{364}{365}\times \frac{363}{365}$
  • t People:
    • $P(\text{no collision among t})=(1-\frac{1}{365})\times (1-\frac{2}{365})\times \cdots \times (1-\frac{t-1}{365})$
• Calculating Probability of At Least One Collision:
  • $P(\text{at least one collision})=1-P(\text{no collision among t})$
• Result for 50% Chance: For $t=23$ people:
  • $P(\text{at least one collision})=1-[(1-\frac{1}{365})\times \cdots \times (1-\frac{22}{365})]\approx 1-0.493=0.507\approx 50\%$
• Result for 90% Chance: Achieved with only $t=40$ people.

5.2 Application to Hash Functions

• Analogy Mapping:

  • People → Messages $x_1,x_2,...,x_t$
  • Birthdays → Hash values $h(x_1),h(x_2),...,h(x_t)$
  • Number of days (365) → Number of possible hash values $N=2^n$ (for an $n$-bit` hash)

• Attacker’s Goal (Collision Search): Hash $t$ different messages and check if any two messages $x_i,x_j$ produce the same hash value $h(x_i)=h(x_j)$.

• Probability of No Collision among $t$ Hash Values:

  • $P(\text{no collision})=(1-\frac{1}{2^n})\times (1-\frac{2}{2^n})\times \cdots \times (1-\frac{t-1}{2^n})$
  • Using product notation: $P(\text{no collision})={\prod }_{i=1}^{t-1}(1-\frac{i}{2^n})$

• Approximation for Probability:

  1. Recall the approximation $e^{-x}\approx 1-x$ for small $x$. Since $i/2^n\ll 1$ for typical $i$ and large $n$, we can use this.
  2. $P(\text{no collision})\approx {\prod }_{i=1}^{t-1}{e}^{-i/2^n}$
  3. $P(\text{no collision})\approx e^{-{\sum }_{i=1}^{t-1}(i/2^n)}=e^{-\frac{1}{2^n}{\sum }_{i=1}^{t-1}i}$
  4. The arithmetic series sum is ${\sum }_{i=1}^{t-1}i=1+2+\cdots +(t-1)=\frac{(t-1)t}{2}$.
  5. Substituting the sum: $P(\text{no collision})\approx e^{-\frac{t(t-1)}{2\cdot 2^n}}=e^{-\frac{t(t-1)}{2^{n+1}}}$

• Finding the Number of Messages $t$ Needed for a Collision:

  1. Let $\lambda$ be the desired probability of finding at least one collision.
  2. $\lambda =P(\text{at least one collision})=1-P(\text{no collision})$
  3. $\lambda \approx 1-e^{-\frac{t(t-1)}{2^{n+1}}}$
  4. $1-\lambda \approx e^{-\frac{t(t-1)}{2^{n+1}}}$
  5. Take the natural logarithm: $\ln (1-\lambda )\approx -\frac{t(t-1)}{2^{n+1}}$
  6. $\frac{t(t-1)}{2^{n+1}}\approx -\ln (1-\lambda )=\ln (\frac{1}{1-\lambda })$
  7. $t(t-1)\approx 2^{n+1}\ln (\frac{1}{1-\lambda })$
  8. For large $t$ (which is typical in practice), $t\gg 1$, so $t^2\approx t(t-1)$.
  9. $t^2\approx 2^{n+1}\ln (\frac{1}{1-\lambda })$
  10. $t\approx \sqrt{2^{n+1}\ln (\frac{1}{1-\lambda })}$
  11. $t\approx 2^{(n+1)/2}\sqrt{\ln (\frac{1}{1-\lambda })}$ (Equation 11.1)

• Most Important Consequence of Birthday Attack:

  • The number of messages $t$ needed to find a collision with a reasonable probability is roughly proportional to the square root of the number of possible output values ($N=2^n$).
  • $t\approx \sqrt{N}=\sqrt{2^n}=2^{n/2}$
  • Implication: To achieve $x$ bits of security against collision attacks, the hash function needs an output length of $n=2x$ bits.

• Example (80-bit Hash):

  • Hash output length $n=80$ bits.
  • Desired success probability $\lambda =0.5$ (50%).
  • Calculate $t$:
    • $t\approx 2^{(80+1)/2}\sqrt{\ln (\frac{1}{1-0.5})}=2^{81/2}\sqrt{\ln (2)}$
    • $t\approx 2^{40.5}\sqrt{0.693}\approx 2^{40.5}\times 0.832$
    • Since $2^{-0.26}\approx 0.832$, $t\approx 2^{40.5}\times 2^{-0.26}=2^{40.24}$
    • So, approximately $t\approx 2^{40.2}$ messages need to be hashed. This confirms the $2^{n/2}$ estimate ($2^{80/2}=2^{40}$).

6. Hash Functions Based on Cipher Block Chaining (CBC)

• Concept: Use a symmetric block cipher (like DES, AES) in a CBC-like mode, but without a secret key, to construct a hash function.
• Rabin’s Proposal [RABI78] (Example):
  1. Divide the message $M$ into fixed-size blocks $M_1,M_2,...,M_N$ (block size matches the cipher’s block size).
  2. Use a symmetric encryption algorithm $E$ (e.g., DES).
  3. Set an initial value $H_0=IV$.
  4. Iterate: $H_i=E(M_i,H_{i-1})$ for $i=1,...,N$.
     • Note: This uses the previous “hash” $H_{i-1}$ as the “key” input to the block cipher for encrypting the current message block $M_i$. (Or sometimes $H_i=E(H_{i-1},M_i)$ - the exact structure varies). The formula given is $H_i=E(M_i,H_{i-1})$.
  5. The final hash code is $G=H_N$.
• Similarity to CBC: Resembles Cipher Block Chaining mode of encryption.
• Key Difference: No secret key is used or required.
• Security Considerations:
  • Birthday Attack: Like any hash code, this construction is subject to the birthday attack.
  • Vulnerability Example (DES): If DES (which has a $64$-bit block size and thus produces a $64$-bit` hash code in this construction) is used, the system is vulnerable. Finding collisions requires only about $2^{64/2}=2^{32}$ operations, which is computationally feasible.