Message Authentication Codes Short Notes

Introduction to MACs

• A Message Authentication Code (MAC), also known as a cryptographic checksum or a keyed hash function, is a widely used cryptographic primitive.
• Functionality: MACs provide:
  • Message Integrity: Ensuring a message has not been altered during transmission.
  • Message Authentication: Verifying the origin of the message (authenticating the sender).
• Basis: MAC algorithms are typically based on either:
  • Symmetric Block Ciphers (e.g., AES)
  • Cryptographic Hash Functions (e.g., SHA-256)

MACs vs. Digital Signatures

Feature	MACs	Digital Signatures
Key Type	Symmetric (shared secret key $k$)	Asymmetric (private key for signing, public key for verification)
Functionality	Integrity, Authentication	Integrity, Authentication, Non-repudiation
Non-repudiation	No - Cannot prove origin to a third party	Yes - Sender cannot deny sending the message
Speed	Generally much faster	Generally slower
Basis	Block ciphers or hash functions	Asymmetric algorithms (e.g., RSA, ECC)

• Advantage of MACs: Speed, due to reliance on faster symmetric-key operations or hash functions.

12.1 Principles of Message Authentication Codes

• Core Idea: Similar to digital signatures, MACs append an authentication tag (the MAC value) to a message $x$.
• Key Difference: MACs use a symmetric key $k$, shared between the sender and receiver, for both generating and verifying the tag.
• Notation: The MAC tag $m$ generated for a message $x$ using key $k$ is denoted as: $m={\text{MAC}}_k(x)$

MAC Process (Generation and Verification)

• Motivation: To allow communicating parties (e.g., Alice and Bob) who share a secret key $k$ to detect any manipulation of a message $x$ sent between them.
• Diagram Description (Fig. 12.1):
  1. Sender (e.g., Bob):
     • Has the message $x$ and the shared secret key $k$.
     • Computes the MAC tag: $m={\text{MAC}}_k(x)$.
     • Sends the message and the tag pair $(x,m)$ to the receiver.
  2. Receiver (e.g., Alice):
     • Receives the pair $(x,m)$.
     • Has the same shared secret key $k$.
     • Independently re-computes the MAC tag using the received message $x$: $m^{\prime }={\text{MAC}}_k(x)$.
     • Verification: Compares the received tag $m$ with the re-computed tag $m^{\prime }$. If $m^{\prime }=m$, the message is considered authentic and integral. If $m^{\prime }\ne m$, the message has been tampered with or did not originate from a party knowing $k$.

Security Services Provided by MACs

1. Message Integrity: The fundamental assumption is that if the message $x$ is altered in transit (maliciously or accidentally), the re-computed MAC $m^{\prime }$ will not match the original MAC $m$. This detects the alteration.
2. Message Authentication: Since only parties possessing the secret key $k$ can compute a valid MAC for a given message $x$, the receiver (Alice) is assured that the message originated from the sender (Bob) who also possesses $k$. An adversary (Oscar) without $k$ cannot create a valid $(x^{\prime },m^{\prime })$ pair for a modified or new message $x^{\prime }$.

Properties of Message Authentication Codes

1. Cryptographic Checksum: A MAC generates a secure, key-dependent checksum (the tag $m$) for a message $x$.
2. Symmetric: MACs rely on shared secret keys. Both the party generating the MAC and the party verifying it must possess the same key $k$.
3. Arbitrary Message Size: MAC algorithms can process input messages $x$ of any length.
4. Fixed Output Length: The generated MAC tag $m$ has a fixed bit length, regardless of the input message size. This length depends on the specific MAC algorithm used.
5. Message Integrity: As described above, MACs allow detection of message modifications.
6. Message Authentication: As described above, MACs assure the receiver of the message’s origin (from someone holding the key $k$).
7. No Non-repudiation: This is a crucial limitation. Because the key $k$ is shared, either party (Alice or Bob) could have generated a specific $(x,m)$ pair. Therefore, neither party can prove to a neutral third party (e.g., a judge) that the other party created the message and MAC. The judge cannot distinguish who generated it. MACs protect the two parties from outsiders, but not from each other in disputes.

12.2 MACs from Hash Functions: HMAC

• One common way to construct MACs is by using cryptographic hash functions (e.g., SHA-1, SHA-256) as the core building block.
• HMAC (Hash-based Message Authentication Code) is a very popular and widely used standard (e.g., in TLS, IPsec).

Basic (Insecure) Hash-Based Constructions

The most intuitive idea is to simply hash the key $k$ and the message $x$ together. The symbol $||$ denotes concatenation.

1. Secret Prefix MAC: $m={\text{MAC}}_k(x)=h(k||x)$
2. Secret Suffix MAC: $m={\text{MAC}}_k(x)=h(x||k)$

• Warning: While seemingly secure due to hash function properties (one-wayness, collision resistance), these simple constructions have security weaknesses.

Attacks Against Secret Prefix MACs (Length Extension Attack)

• Assumption: This attack applies when the underlying hash function $h$ uses an iterative structure like Merkle-Damgård (common in MD5, SHA-1, SHA-2). The message $x$ is processed in blocks: $x=(x_1,x_2,...,x_n)$.
• Process: Bob computes $m=h(k||x_1||x_2||...||x_n)$. The value $m$ is the final hash output.
• The Attack: An adversary Oscar, who intercepts $(x,m)$, can compute a valid MAC $m^{\prime }$ for a new message $x^{\prime }=x||\text{padding}||x_{n+1}$ (where $x_{n+1}$ is an arbitrary block chosen by Oscar) without knowing the secret key $k$.
• How it works: The output $m$ of $h(k||x)$ represents the internal state of the hash function after processing $k$ and $x$. Oscar can use $m$ as the initial state (IV) for hashing additional data ($x_{n+1}$, along with necessary padding derived from the original message length). The result $m^{\prime }$ will be the correct MAC for the extended message $x^{\prime }$.
• Diagram Explanation (Implied by Attack Description & Figure on p.323):
  1. Oscar intercepts $(x,m)$ where $m=h(k||x)$.
  2. Oscar chooses an extension block $x_{n+1}$.
  3. Oscar computes the necessary padding for the original message $x$ based on its length (this might be implicitly handled by the hash continuation).
  4. Oscar computes $m^{\prime }=h(m||\text{padding}||x_{n+1})$ (conceptually, continuing the hash from state $m$).
  5. Oscar sends the forged message $x^{\prime }=(x||\text{padding}||x_{n+1})$ and the forged MAC $m^{\prime }$ to Alice.
  6. Alice, upon receiving $(x^{\prime },m^{\prime })$, computes ${\text{MAC}}_k(x^{\prime })=h(k||x||\text{padding}||x_{n+1})$. Due to the iterative nature, this computation yields $m^{\prime }$, so Alice accepts the forged message.
• Consequence: This is serious. For example, Oscar could append unfavorable clauses to an electronic contract $x$ and compute a valid MAC for the modified contract $x^{\prime }$.

Attacks Against Secret Suffix MACs

• Construction: $m={\text{MAC}}_k(x)=h(x||k)$
• Weakness: The security of this construction can be limited by the collision resistance of the underlying hash function $h$, independent of the key $k$.
• The Attack (Birthday Attack based):
  • If an attacker Oscar can find a collision for the hash function $h$ itself (i.e., find two different messages $x$ and $x_0$ such that $h(x)=h(x_0)$), this may compromise the MAC. (Note: The text’s claim that $m=h(x||k)$ is also valid for $x_0$ just because $h(x)=h(x_0)$ is not generally true for the suffix method, but the underlying security concern is valid).
  • More accurate concern: The security level might be lower than expected based on the key length $|k|$. Finding a collision for a hash function with an $l$-bit output using a birthday attack takes approximately $O(2^{l/2})$ operations.
  • If $2^{l/2}$ is less than $2^{|k|}$ (the complexity of brute-forcing the key), then an attacker might target the hash function’s collision resistance rather than the key.
• Example: Using SHA-1 ($l=160$ bits) with a $128$-bit key ($|k|=128$).
  • Brute-force key search takes $O(2^{128})$ operations.
  • Finding a SHA-1 collision takes roughly $O(2^{160/2})=O(2^{80})$ operations (and possibly fewer due to known weaknesses).
  • In this case, the effective security is limited by the $\approx 2^{80}$ complexity of the collision attack on the hash function, not the $2^{128}$ strength suggested by the key length.

HMAC Construction

• Proposed by Bellare, Canetti, and Krawczyk (1996) to overcome the weaknesses of the simpler prefix/suffix constructions.
• Structure: Uses two nested hash computations (inner and outer). Let $h$ be the hash function, $k$ be the secret key, and $x$ be the message. Let $b$ be the input block size of the hash function in bits, and $l$ be the output size in bits.

HMAC Steps & Diagram Description (Fig 12.2)

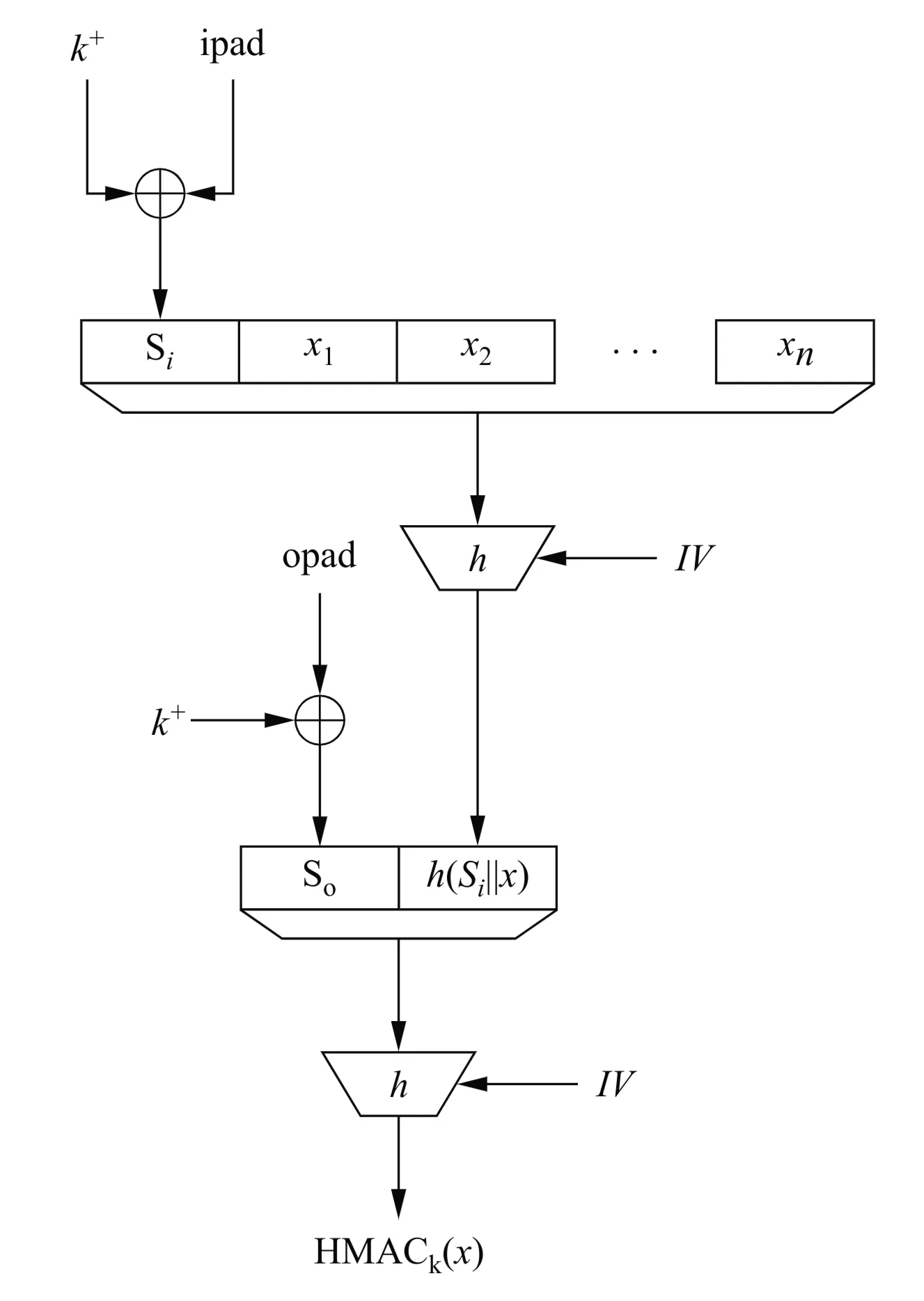
1. Key Preparation:
   • If the key $k$ is longer than the block size $b$, hash the key first: $k=h(k)$.
   • If the key $k$ (or hashed $k$) is shorter than $b$ bits, pad it with zeros on the left to create a $b$-bit block $k^{+}$.
   • If $k$ is exactly $b$ bits, $k^{+}=k$.
2. Define Pads: Two constant $b$-bit strings are used:
   • ipad (inner pad): Byte 0x36 repeated $b/8$ times. (Binary: 00110110...)
   • opad (outer pad): Byte 0x5C repeated $b/8$ times. (Binary: 01011100...)
3. Inner Hash:
   • Compute the $b$-bit block $S_i=k^{+}\oplus \text{ipad}$.
   • Concatenate $S_i$ with the message $x$: $S_i||x$.
   • Compute the hash: $H_{inner}=h(S_i||x)$. (The hash function’s IV is used here).
4. Outer Hash:
   • Compute the $b$-bit block $S_o=k^{+}\oplus \text{opad}$.
   • Concatenate $S_o$ with the result of the inner hash: $S_o||H_{inner}$.
   • Compute the hash: $H_{outer}=h(S_o||H_{inner})$. (The hash function’s IV is used again here).
5. Result: The HMAC is the output of the outer hash: ${\text{HMAC}}_k(x)=H_{outer}$

HMAC Formula

The entire construction can be expressed as:

${\text{HMAC}}_k(x)=h((k^{+}\oplus \text{opad})||h((k^{+}\oplus \text{ipad})||x))$

• Note on Sizes: Often, the hash output length $l$ is smaller than the block size $b$ (e.g., SHA-1: $l=160$, $b=512$). The inner hash result $H_{inner}$ (length $l$) needs to be processed by the outer hash, which expects $b$-bit blocks. Hash functions inherently handle this through their padding and preprocessing steps defined in their standards (e.g., Section 11.4.1 for SHA-1 preprocessing).

HMAC Efficiency

• The potentially long message $x$ is hashed only once (in the inner hash).
• The outer hash operates on only two blocks: the derived outer key $S_o$ and the inner hash result $H_{inner}$.
• The computational overhead compared to simply hashing the message is minimal (one extra hash computation on short, fixed-size blocks).

HMAC Security

• HMAC has a proof of security.
• Its security is formally related to the security properties of the underlying hash function $h$.
• Result: If the hash function $h$ meets certain requirements (primarily pseudorandomness when keyed via the HMAC structure, related to collision resistance and preimage resistance), then HMAC is a secure MAC.
• Specifically, it can be shown that an attacker able to break HMAC (e.g., forge a MAC without the key, distinguish HMAC output from random) could also be used to break the underlying hash function (e.g., find collisions, compute hash output without knowing the initial state/IV).

12.3 MACs from Block Ciphers: CBC-MAC

• An alternative to hash-based MACs is to use symmetric block ciphers (like AES).
• The most common method is based on the Cipher Block Chaining (CBC) mode of operation, hence CBC-MAC.

MAC Generation (CBC-MAC)

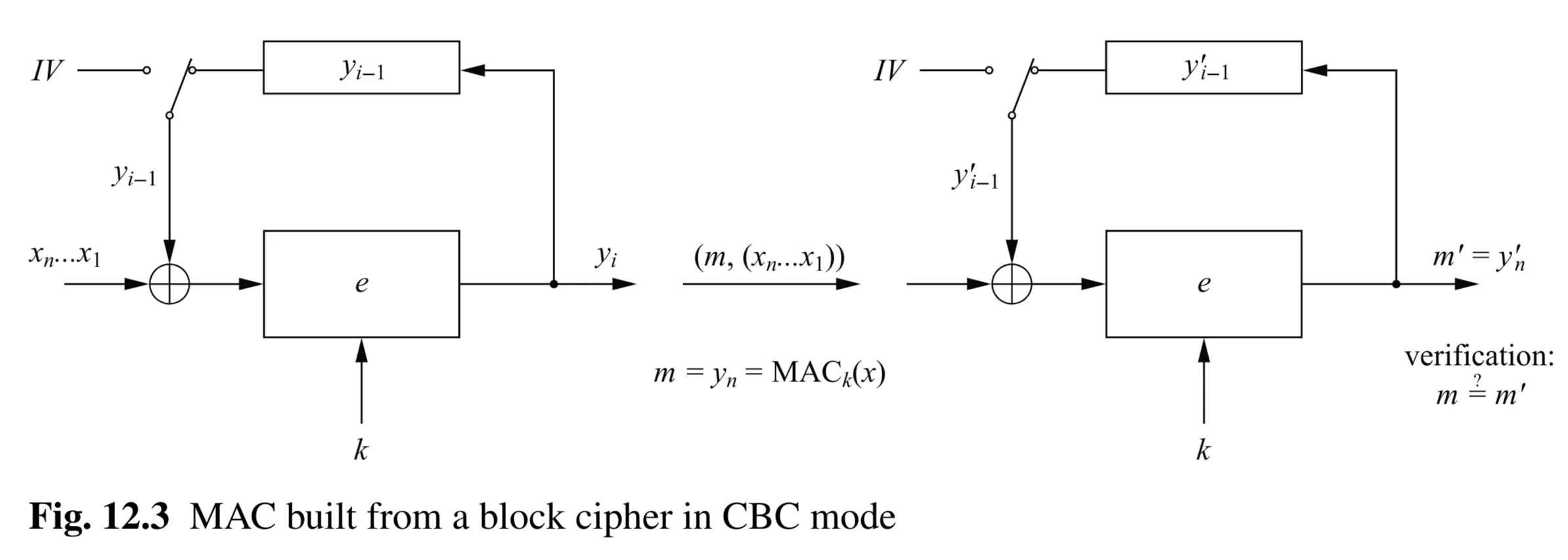
• Setup: Requires a block cipher encryption function $e$, a secret key $k$, and an Initial Value $IV$. The message $x$ is divided into blocks $x_1,x_2,...,x_n$ matching the block cipher’s block size.
• Process (Diagram Fig 12.3 - Left/Sender):
  1. First Block: Compute $y_1=e_k(x_1\oplus IV)$.
  2. Subsequent Blocks ($i=2$ to $n$): Compute $y_i=e_k(x_i\oplus y_{i-1})$. (The output of the previous encryption block is XORed with the current message block before encrypting).
  3. Final MAC: The MAC tag $m$ is the entire output of the last encryption: $m={\text{MAC}}_k(x)=y_n$.
• Important Notes:
  • The $IV$ can be public, but should ideally be unpredictable (random or nonce) for certain security proofs, though a fixed IV (e.g., IV=0) is common in basic CBC-MAC standards (with security implications if not handled carefully, especially regarding message prefixes).
  • The intermediate values $y_1,y_2,...,y_{n-1}$ are internal state and are not transmitted or revealed. Only the final $y_n$ is the MAC.

MAC Verification (CBC-MAC)

• Process (Diagram Fig 12.3 - Right/Receiver):
  1. The receiver gets the message $x$ and the MAC tag $m$.
  2. Using the same shared secret key $k$, the same $IV$, and the received message blocks $x_1,...,x_n$, the receiver performs the exact same CBC-MAC computation as the sender:
     • $y_1^{\prime }=e_k(x_1\oplus IV)$
     • $y_i^{\prime }=e_k(x_i\oplus y_{i-1}^{\prime })$ for $i=2,...,n$.
  3. This yields a computed tag $m^{\prime }=y_n^{\prime }$.
  4. Verification: Compare the computed tag $m^{\prime }$ with the received tag $m$.
     • If $m^{\prime }=m$, the MAC is valid; accept the message.
     • If $m^{\prime }\ne m$, the MAC is invalid; reject the message (it was altered or forged).