Levels of Key Establishment

Level 1: The “Why” and “What” of Key Establishment

What’s the Big Deal with Keys?

You’ve learned about powerful cryptographic tools:

• Confidentiality: Keeping secrets using encryption (symmetric or asymmetric).
• Integrity: Ensuring data isn’t tampered with (using MACs or digital signatures).
• Authentication: Verifying who sent a message (using MACs or digital signatures).
• Non-repudiation: Proving someone sent a message and can’t deny it (using digital signatures).

The Catch: ALL these tools rely on keys.

• Symmetric methods (AES, MACs) need Alice and Bob to share the exact same secret key.
• Asymmetric methods (RSA, signatures) need Alice to know Bob’s authentic public key and vice-versa.

Getting these keys to the right people securely before you can even start encrypting or signing is a fundamental challenge. This process is called Key Establishment.

Two Main Flavors of Key Establishment

Think about how Alice and Bob could end up with a shared secret key: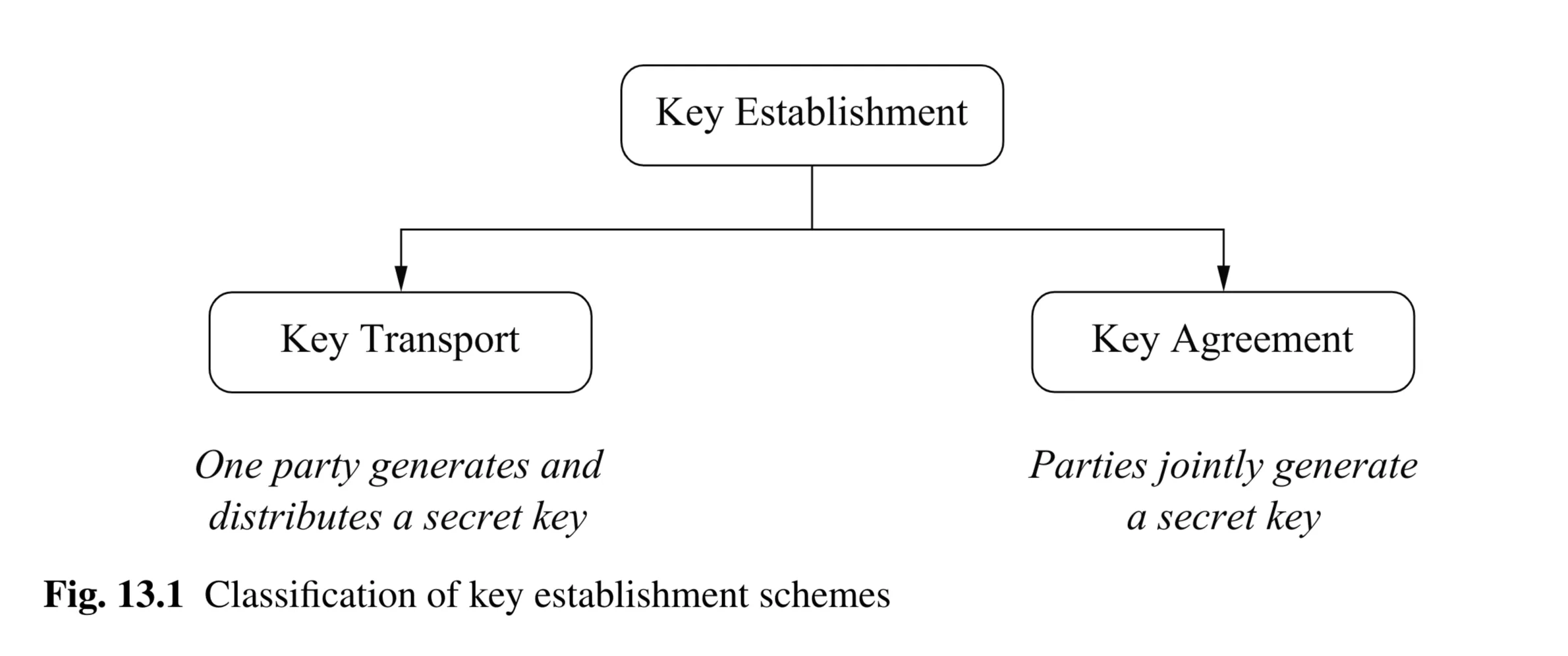

1. Key Transport: Alice creates a secret key, then securely sends it to Bob. Alice is in control of the key value initially.
2. Key Agreement: Alice and Bob work together, exchanging some information publicly, and both derive the same shared secret key independently. Ideally, neither party alone controls the final key value. (Diffie-Hellman is the classic example you might have seen).

The Headache of Scaling Up: The $n^2$ Problem

Imagine a small group of 4 people (Alice, Bob, Chris, Dana) who all want to talk securely with each other using symmetric keys.

• Alice needs a key for Bob ($K_{AB}$), for Chris ($K_{AC}$), and for Dana ($K_{AD}$). That’s 3 keys for Alice.
• Bob needs keys for Alice ($K_{BA}=K_{AB}$), Chris ($K_{BC}$), and Dana ($K_{BD}$).
• …and so on.

The Problem:

• Each person needs to store $n-1$ keys (where $n$ is the number of people).
• The total number of unique key pairs in the network is $n(n-1)/2$. This grows quadratically (roughly $n^2$).
• For 4 users: $4\ast 3/2=6$ unique keys ($K_{AB},K_{AC},K_{AD},K_{BC},K_{BD},K_{CD}$).
• For 750 users (Example 13.1): $750\ast 749/2=280,875$ unique keys!
• Worse: If a new person (Noah) joins, you need to establish a new secure key between Noah and every single existing person. This requires $n$ new secure key distributions.

Manually distributing keys (e.g., on a USB stick, over the phone - “out-of-band”) works for very small, static groups but breaks down quickly. We need better methods.

Key Takeaway Level 1: Key establishment is crucial but non-trivial. Simple manual distribution doesn’t scale. We need automated, secure ways to transport or agree on keys.

---

Level 2: Using a Helper - The Key Distribution Center (KDC)

Solving the $n^2$ Problem with a Trusted Friend

Instead of everyone managing keys with everyone else, what if we introduce a trusted central server? Let’s call it the Key Distribution Center (KDC).

The Setup:

1. Every user (Alice, Bob, …) trusts the KDC completely.
2. When a user joins the network initially, they establish one secret key just between them and the KDC. This is called a Key Encryption Key (KEK).
   • Alice has $K_A$ (shared only with KDC).
   • Bob has $K_B$ (shared only with KDC).
   • The KDC stores all these KEKs ($K_A,K_B,K_C,...$).
   • This initial KEK distribution still needs a secure channel (like manual setup), but it’s only one key per user joining, not $n-1$.

Basic KDC Protocol (Key Transport)

Now, how does Alice get a key to talk to Bob?

1. Request: Alice tells the KDC, “I ($I{D}_A$) want to talk to Bob ($I{D}_B$).” (RQST(IDA, IDB))
2. KDC Action:
   • The KDC generates a brand new, random key for this specific conversation. This is called a session key ($k_{ses}$). Session keys are temporary (more on this later).
   • The KDC encrypts this session key twice:
     • Once using Alice’s KEK: $y_A=e_{K_A}(k_{ses})$
     • Once using Bob’s KEK: $y_B=e_{K_B}(k_{ses})$
3. Distribution: The KDC sends $y_A$ to Alice and $y_B$ to Bob. (Or sends both to Alice, who forwards $y_B$ to Bob).
4. Decryption:
   • Alice uses her KEK $K_A$ to decrypt $y_A$ and get $k_{ses}$.
   • Bob uses his KEK $K_B$ to decrypt $y_B$ and get $k_{ses}$.
5. Success! Alice and Bob now share $k_{ses}$ and can communicate securely using it.

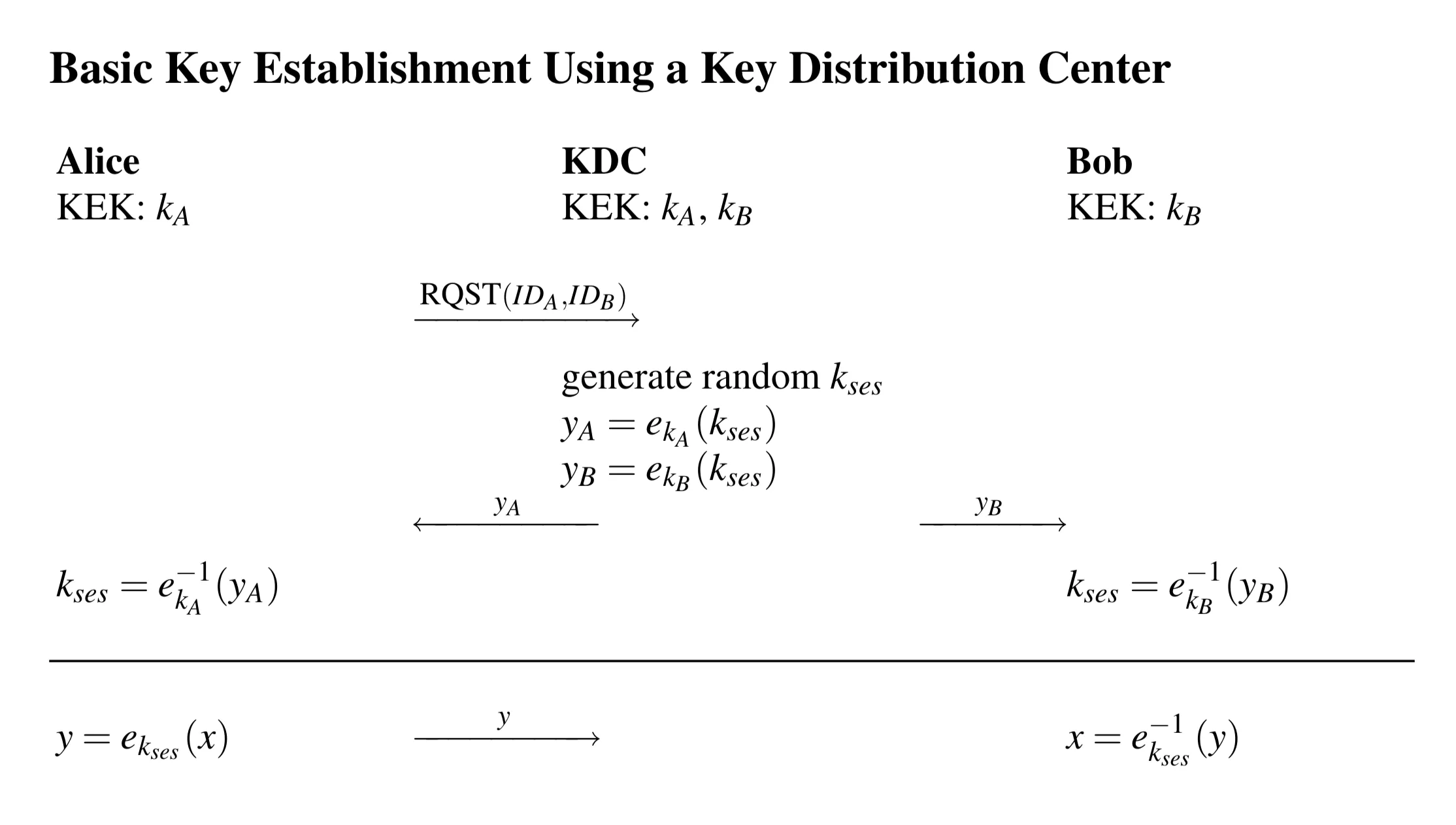
Key Advantage: Only $n$ long-term KEKs are needed. Adding a user requires only establishing one new KEK with the KDC. Much better than $n^2$.

Key Freshness and Key Derivation

Why use temporary session keys?

• Damage Limitation: If a session key $k_{ses}$ is somehow compromised (e.g., attacker guesses it later), only the communication protected by that specific key is revealed. Past and future sessions (using different session keys) remain secure.
• Attack Difficulty: An attacker has less ciphertext encrypted with any single key, making cryptanalysis harder.

How to get fresh keys without contacting the KDC every single time? If Alice and Bob already share a key $K_{AB}$ (maybe it’s a KEK, or a previously established session key they want to update), they can derive a new session key ($k_{ses}$) from it.

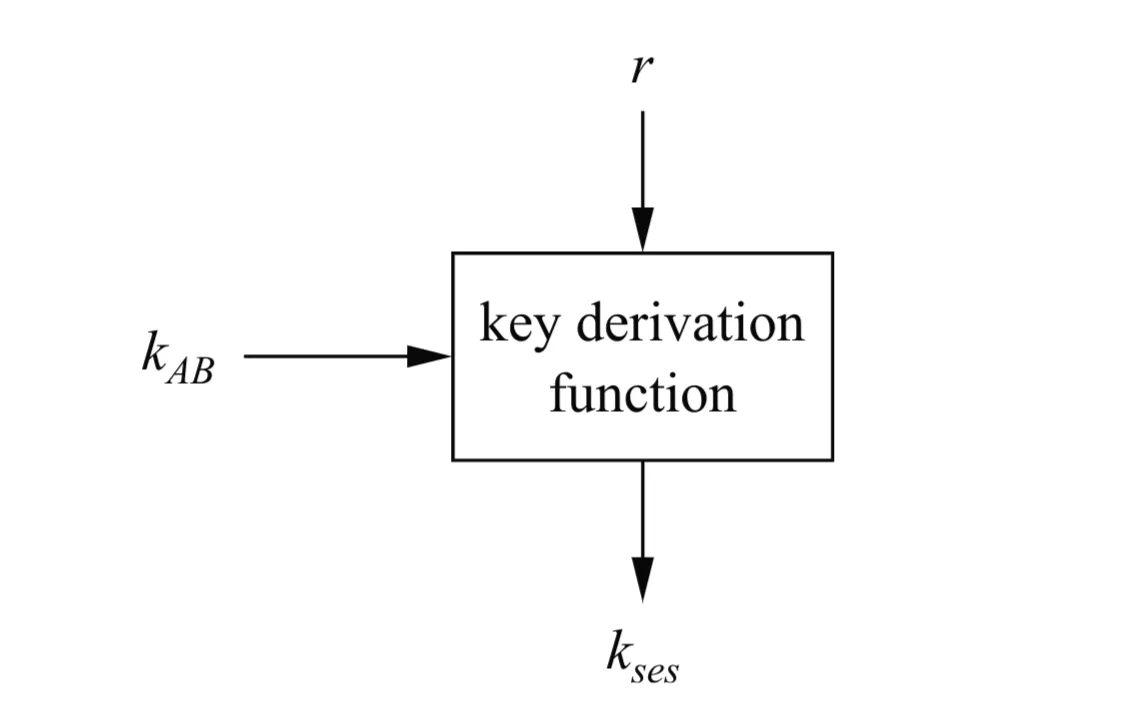Shows a box labeled “key derivation function” (KDF).

• Inputs: The existing shared secret $K_{AB}$ and some non-secret changing value $r$.
• Output: The new session key $k_{ses}$.

Methods:

1. Nonce-based: One party (say Bob) generates a random number, used only once (a nonce), $r$. He sends $r$ to Alice. Both compute $k_{ses}=\text{KDF}(K_{AB},r)$. A common KDF is encryption: $k_{ses}=e_{K_{AB}}(r)$ or using a MAC: $k_{ses}={\text{HMAC}}_{K_{AB}}(r)$.
2. Counter-based: If Alice and Bob can keep synchronized counters ($cnt$), they can both compute $k_{ses}=\text{KDF}(K_{AB},cnt)$ periodically, incrementing the counter each time. $k_{ses}=e_{K_{AB}}(cnt)$ or $k_{ses}={\text{HMAC}}_{K_{AB}}(cnt)$. This avoids sending the nonce $r$.

Important KDF Property: The KDF must be a one-way function. Knowing $k_{ses}$ and $r$ (or $cnt$) should NOT allow an attacker to figure out the original $K_{AB}$. This protects the master key even if session keys leak.

Key Takeaway Level 2: KDCs centralize trust and key management, solving the $n^2$ problem for symmetric keys. They use long-term KEKs to securely transport short-term session keys. Session keys provide freshness and limit damage. Key derivation functions can generate new keys from existing ones.

---

Level 3: Making KDCs Robust - Kerberos and Security Concerns

Problems with the Basic KDC Protocol

The simple KDC protocol (Level 2) is conceptually nice, but vulnerable to active attackers (who can intercept, modify, and inject messages).

1. Replay Attack: Suppose Oscar eavesdropped on a past session and recorded $y_A$ and $y_B$ (containing an old session key, $k_{ses,old}$) that Alice and Bob used. If $k_{ses,old}$ later becomes compromised (e.g., Alice’s computer gets hacked), Oscar can simply resend the old $y_A$ to Alice and $y_B$ to Bob. They will decrypt them, recover $k_{ses,old}$, and think they have established a fresh session. Oscar, knowing $k_{ses,old}$, can now decrypt their “new” communication or even impersonate Alice or Bob. The basic protocol lacks timeliness or freshness checks.

2. Key Confirmation Attack (Impersonation): Alice wants to talk to Bob. She sends RQST(IDA, IDB) to the KDC. Malicious user Oscar intercepts this. He sends RQST(IDA, IDO) (claiming Alice wants to talk to him) to the KDC. The KDC, doing its job, generates a $k_{ses}$ and sends back $y_A=e_{K_A}(k_{ses})$ and $y_O=e_{K_O}(k_{ses})$. Oscar intercepts these. He forwards $y_A$ to Alice. Alice decrypts it and gets $k_{ses}$. Oscar also decrypts $y_O$ with his key $K_O$ and gets the same $k_{ses}$. Now, Alice thinks the key $k_{ses}$ she received is for talking to Bob (because that’s who she asked for), but the KDC actually generated it for a session between Alice and Oscar. When Alice sends a message encrypted with $k_{ses}$, supposedly to Bob, Oscar can intercept and decrypt it because he also has $k_{ses}$. Alice has no way to confirm that the key she received is actually associated with Bob.

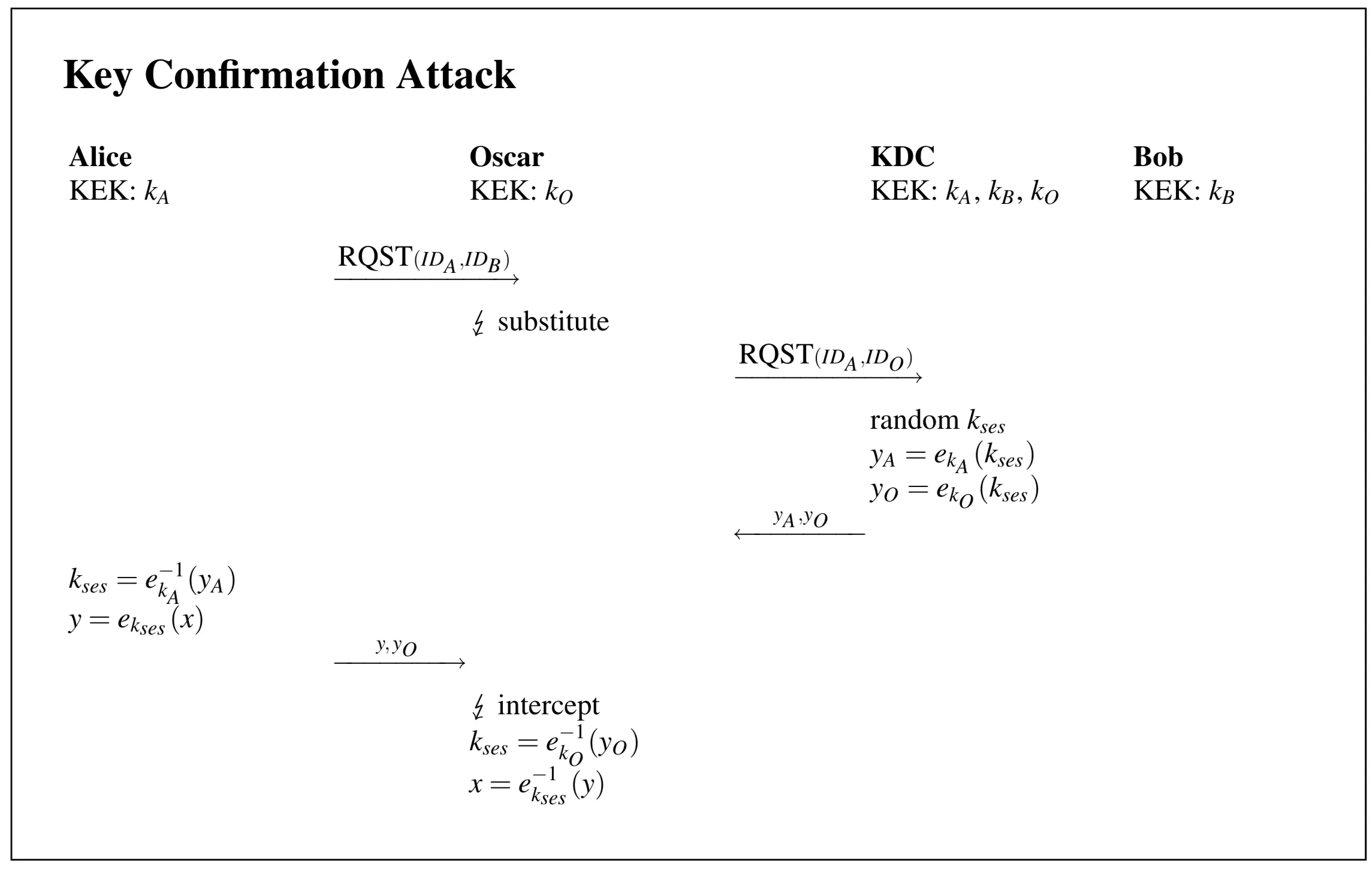This illustrates the Key Confirmation Attack:

• Alice sends RQST(IDA, IDB).
• Oscar intercepts, substitutes RQST(IDA, IDO) and sends to KDC.
• KDC generates $k_{ses}$, creates $y_A=e_{K_A}(k_{ses})$ and $y_O=e_{K_O}(k_{ses})$. Sends $y_A,y_O$ back (intended for Alice and Oscar).
• Oscar intercepts $y_A,y_O$. He forwards only $y_A$ to Alice.
• Alice decrypts $y_A$ gets $k_{ses}$. She thinks this is for Bob.
• Oscar decrypts $y_O$ gets $k_{ses}$.
• Alice encrypts message $x$ as $y=e_{k_{ses}}(x)$ (intending to send to Bob).
• Oscar intercepts $y$ and decrypts it using $k_{ses}$.

Kerberos: A More Secure KDC Protocol

Kerberos is a widely used authentication and key distribution protocol (used in Windows networks, for example) that addresses these flaws. Here’s a simplified view:

Key Ideas:

• Timeliness: Uses timestamps and lifetimes to prevent replays.
• Authentication & Confirmation: Includes identities and nonces within encrypted messages to ensure parties know who they are talking to and that messages are fresh.

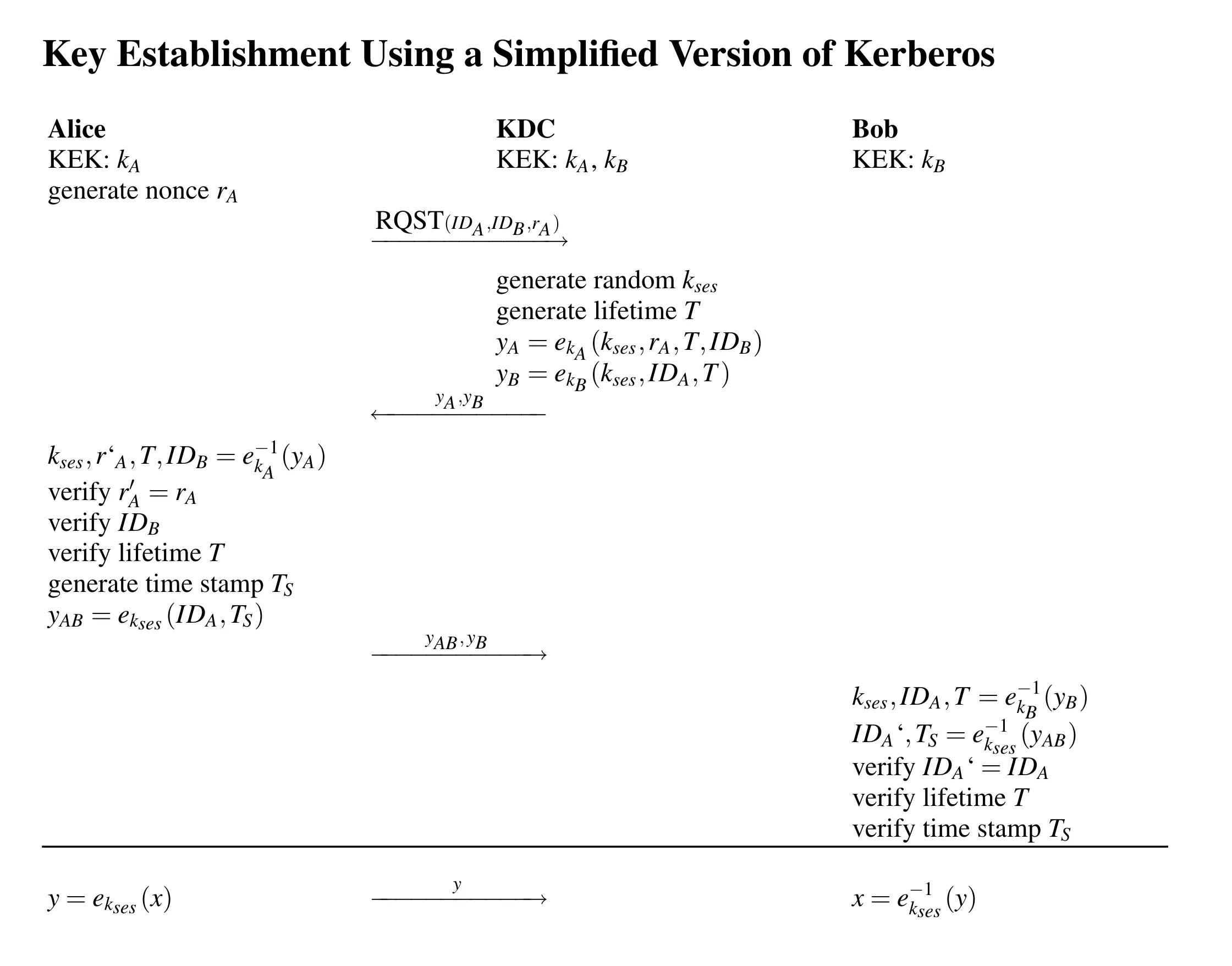
1. Alice → KDC: Alice sends her ID ($I{D}_A$), Bob’s ID ($I{D}_B$), and a nonce $r_A$ (a random number she just generated). RQST(IDA, IDB, rA)
2. KDC → Alice: KDC generates $k_{ses}$ and a lifetime $T$ (how long $k_{ses}$ is valid). It sends back two pieces:
   • Session Info for Alice: $y_A=e_{K_A}(k_{ses},r_A,T,I{D}_B)$. Encrypted with Alice’s KEK. Contains the session key, her original nonce $r_A$, the lifetime $T$, and Bob’s ID.
   • Ticket for Bob (TGT): $y_B=e_{K_B}(k_{ses},I{D}_A,T)$. Encrypted with Bob’s KEK. Contains the session key, Alice’s ID, and the lifetime $T$. (This is like a sealed envelope only Bob can open).
3. Alice’s Actions:
   • Decrypts $y_A$ using $K_A$.
   • Checks $r_A$: Does the nonce match the one she sent? If yes, she knows this message is a fresh reply from the KDC (not a replay) because only she and the KDC knew $r_A$. This authenticates the KDC to Alice.
   • Checks $I{D}_B$: Is this the ID of the person she wanted to talk to? If yes, she knows the KDC generated the key for the right session.
   • Stores $k_{ses}$ and $T$.
   • Creates an Authenticator: $y_{AB}=e_{k_{ses}}(I{D}_A,T_S)$. Encrypts her ID and the current timestamp $T_S$ using the new session key $k_{ses}$.
4. Alice → Bob: Alice sends Bob the Ticket ($y_B$) and the Authenticator ($y_{AB}$).
5. Bob’s Actions:
   • Decrypts the Ticket $y_B$ using his KEK $K_B$. Gets $k_{ses}$, $I{D}_A$, and $T$.
   • Decrypts the Authenticator $y_{AB}$ using the $k_{ses}$ he just extracted. Gets $I{D}_A^{\prime }$ and $T_S$.
   • Checks $I{D}_A$: Does $I{D}_A^{\prime }$ from the authenticator match $I{D}_A$ from the ticket? Confirms the authenticator is linked to this ticket.
   • Checks Timestamp $T_S$: Is $T_S$ recent (e.g., within 5 minutes of Bob’s clock)? Prevents replay of the authenticator. Requires loosely synchronized clocks.
   • Checks Lifetime $T$: Is the ticket still valid according to its lifetime?
   • If all checks pass, Bob trusts that the key $k_{ses}$ is fresh, valid, and shared with the user identified as $I{D}_A$. He now has the session key.

Kerberos Solves the Problems:

• Replay: Prevented by Alice checking nonce $r_A$ and Bob checking timestamp $T_S$. Old messages/tickets will fail these checks.
• Key Confirmation: Alice confirms she’s getting a key for Bob (checks $I{D}_B$ in $y_A$). Bob confirms the key came from Alice (checks $I{D}_A$ in $y_B$ and $y_{AB}$).

Lingering Problems with KDC-Based Systems

Even with Kerberos, some fundamental issues remain:

1. Single Point of Failure: The KDC holds all the KEKs. If the KDC server is compromised, the entire system is broken. All communication can potentially be decrypted.
2. Secure Channel for Initialization: Still need a secure way to distribute the initial KEK ($K_A,K_B$, etc.) to each user when they join.
3. No Perfect Forward Secrecy (PFS): This is a subtle but important one. Suppose Oscar records all encrypted traffic between Alice and Bob over months. Later, he manages to steal Alice’s long-term KEK ($K_A$). Using $K_A$, he can go back and decrypt all the past $y_A$ messages she received from the KDC, recover all the old session keys ($k_{ses}$), and then decrypt all the recorded conversations.
   • Definition 13.1: Perfect Forward Secrecy (PFS) means that compromising long-term keys (like KEKs) does NOT compromise past session keys.
   • KDC-based systems like Kerberos generally do not provide PFS because the session keys are derived directly from (or transported encrypted by) the long-term KEKs.

Key Takeaway Level 3: Basic KDC protocols are vulnerable to replay and impersonation attacks. Kerberos adds nonces, timestamps, lifetimes, and identity checks to fix these. However, all KDC systems suffer from a single point of failure (the KDC itself) and typically lack Perfect Forward Secrecy.

---

Level 4: Asymmetric Approach & The Man-in-the-Middle (MIM) Attack

Using Public-Key Crypto for Key Establishment

Public-key cryptography seems like a natural fit for key establishment, especially key agreement:

• Diffie-Hellman Key Exchange (DHKE): Alice and Bob can agree on a shared secret key over an insecure channel without any prior shared secrets.

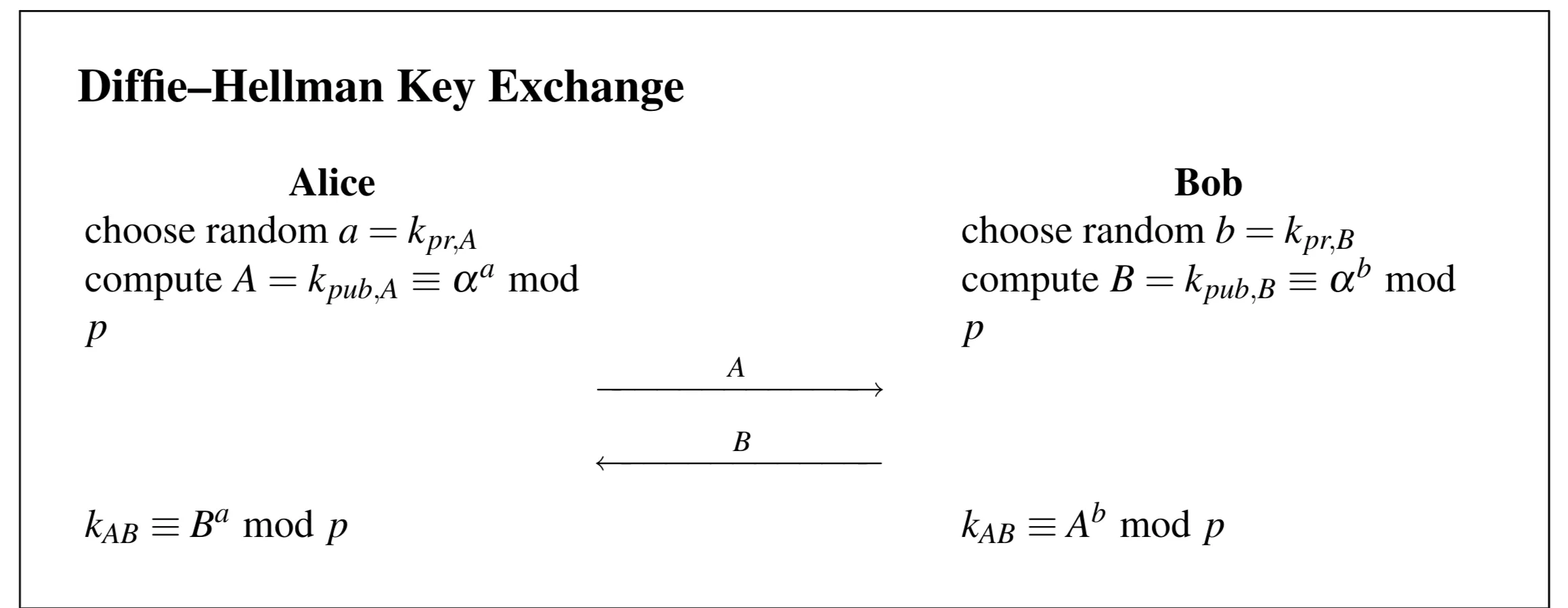
1. Alice and Bob agree publicly on large prime $p$ and generator $\alpha$.
2. Alice chooses private random $a$, computes public $A={\alpha }^a(\mathrm{mod}p)$, sends $A$ to Bob.
3. Bob chooses private random $b$, computes public $B={\alpha }^b(\mathrm{mod}p)$, sends $B$ to Alice.
4. Alice computes shared secret $K_{AB}=B^a=({\alpha }^b{)}^a={\alpha }^{ab}(\mathrm{mod}p)$.
5. Bob computes shared secret $K_{AB}=A^b=({\alpha }^a{)}^b={\alpha }^{ab}(\mathrm{mod}p)$. They arrive at the same key $K_{AB}$. An eavesdropper seeing only $p,\alpha ,A,B$ cannot easily compute $a,b$ or $K_{AB}$ (due to the difficulty of the Discrete Logarithm Problem).

It seems we’ve solved the key establishment problem without needing a KDC or pre-shared keys! … Or have we?

The Man-in-the-Middle (MIM) Attack

DHKE (and other public-key systems used naïvely) is vulnerable to a devastating Man-in-the-Middle (MIM) attack if the public keys ($A$ and $B$) are not authenticated.

How it Works (DHKE Example): Oscar positions himself between Alice and Bob, intercepting all messages.

1. Alice chooses $a$, computes $A={\alpha }^a(\mathrm{mod}p)$. Sends $A$ towards Bob.
2. Oscar intercepts $A$. He chooses his own secret random $o$, computes $\tilde{A}={\alpha }^o(\mathrm{mod}p)$ (or maybe just uses $O={\alpha }^o(\mathrm{mod}p)$ for both directions). Oscar sends $\tilde{A}$ (or $O$) to Bob, pretending it came from Alice.
3. Bob chooses $b$, computes $B={\alpha }^b(\mathrm{mod}p)$. Sends $B$ towards Alice.
4. Oscar intercepts $B$. He computes $\tilde{B}={\alpha }^o(\mathrm{mod}p)$ (or uses the same $O$). Oscar sends $\tilde{B}$ (or $O$) to Alice, pretending it came from Bob.
5. Alice’s Calculation: Alice receives $\tilde{B}$ (thinking it’s $B$). She computes her key as $K_{AO}=(\tilde{B}{)}^a=({\alpha }^o{)}^a={\alpha }^{oa}(\mathrm{mod}p)$. She thinks she shares this key with Bob.
6. Bob’s Calculation: Bob receives $\tilde{A}$ (thinking it’s $A$). He computes his key as $K_{BO}=(\tilde{A}{)}^b=({\alpha }^o{)}^b={\alpha }^{ob}(\mathrm{mod}p)$. He thinks he shares this key with Alice.
7. Oscar’s Calculation: Oscar knows $a$ (no, he knows $A={\alpha }^a$), $b$ (no, he knows $B={\alpha }^b$), and his own secret $o$.
   • He computes the key he shares with Alice: $K_{AO}=A^o=({\alpha }^a{)}^o={\alpha }^{ao}(\mathrm{mod}p)$.
   • He computes the key he shares with Bob: $K_{BO}=B^o=({\alpha }^b{)}^o={\alpha }^{bo}(\mathrm{mod}p)$.

Shows the intercept and substitute flow:

• Alice sends $A\to$ Oscar intercepts. Oscar sends $\tilde{A}$ (his value) $\to$ Bob receives.
• Bob sends $B\to$ Oscar intercepts. Oscar sends $\tilde{B}$ (his value) $\to$ Alice receives.
• Alice computes $K_{AO}=(\tilde{B}{)}^a$. Bob computes $K_{BO}=(\tilde{A}{)}^b$.
• Oscar computes $K_{AO}=A^o$ and $K_{BO}=B^o$.

The Result:

• Alice and Bob think they performed a secure key exchange and share a key $K_{AB}$.
• In reality, Alice shares key $K_{AO}$ with Oscar, and Bob shares key $K_{BO}$ with Oscar.
• Oscar sits in the middle. When Alice sends a message encrypted with $K_{AO}$ (thinking it’s for Bob), Oscar intercepts, decrypts it with $K_{AO}$, reads it (and can modify it!), then re-encrypts it with $K_{BO}$ and sends it to Bob. Bob decrypts it with $K_{BO}$ and thinks it came directly from Alice.

(Diagram Explanation - Fig. 13.12) Illustrates the message relay after the MIM key exchange:

• Alice sends $y={\text{AES}}_{K_{AO}}(x)$.
• Oscar intercepts $y$. Decrypts $x={\text{AES}}_{K_{AO}}^{-1}(y)$. Reads/modifies $x$ to $x^{\prime }$. Re-encrypts $y^{\prime }={\text{AES}}_{K_{BO}}(x^{\prime })$.
• Oscar sends $y^{\prime }$ to Bob.
• Bob receives $y^{\prime }$. Decrypts $x^{\prime }={\text{AES}}_{K_{BO}}^{-1}(y^{\prime })$.

The Core Problem: Alice has no way to verify that the public value $B$ she received actually came from Bob. Bob has no way to verify $A$ came from Alice. Public keys need authentication.

Critical Statement: Even though public-key schemes do not require a secure channel [like symmetric keys initially do], they require authenticated channels for the distribution of the public keys.

Key Takeaway Level 4: Public-key methods like DHKE offer key agreement without pre-shared secrets but are vulnerable to Man-in-the-Middle attacks if the public keys exchanged are not authenticated. Authentication is crucial.

---

Level 5: The Solution - Certificates, PKI, and Trust

Authenticating Public Keys with Digital Signatures: Certificates

How can Alice be sure that the public key $A$ really belongs to Alice? We need to tie an identity ($I{D}_A$) to a public key ($k_{pub,A}$) in a verifiable way. Digital signatures are perfect for this!

The Idea: Certificates

• We need a trusted third party again, but this one doesn’t hold everyone’s secrets. Let’s call it a Certification Authority (CA).
• Everyone trusts the CA. The CA has its own public/private key pair ($k_{pub,CA},k_{pr,CA}$). Everyone knows the CA’s authentic public key $k_{pub,CA}$. (This still needs secure distribution initially, maybe bundled with your OS or browser).
• When Alice wants her public key $k_{pub,A}$ to be trusted, she goes to the CA.
• The CA verifies Alice’s identity ($I{D}_A$) through some real-world process (e.g., checking documents).
• The CA then creates a certificate which contains:
  • Alice’s identity information ($I{D}_A$).
  • Alice’s public key ($k_{pub,A}$).
  • Other info (like validity period).
  • The CA’s digital signature over all this information, created using the CA’s private key $k_{pr,CA}$.

Formal Structure (Simplified): ${\text{Cert}}_A=[({\text{data}}_A),{\text{sig}}_{k_{pr,CA}}({\text{data}}_A)]$ where ${\text{data}}_A=(k_{pub,A},I{D}_A,\text{validity},...)$

How Certificates Prevent MIM: Now, let’s redo DHKE with certificates.

1. Alice generates $a$, $A={\alpha }^a(\mathrm{mod}p)$. She gets her certificate ${\text{Cert}}_A$ from the CA, which includes $A$ and $I{D}_A$, signed by the CA.
2. Bob generates $b$, $B={\alpha }^b(\mathrm{mod}p)$. He gets his certificate ${\text{Cert}}_B$ from the CA, which includes $B$ and $I{D}_B$, signed by the CA.
3. Alice sends ${\text{Cert}}_A$ to Bob. Bob sends ${\text{Cert}}_B$ to Alice.
4. Alice’s Actions:
   • Receives ${\text{Cert}}_B$.
   • Uses the CA’s public key ($k_{pub,CA}$, which she already trusts) to verify the signature on ${\text{Cert}}_B$.
   • If the signature is valid, she knows the CA vouches for the contents. She trusts that the public key $B$ inside the certificate really belongs to the identity $I{D}_B$.
   • She extracts $B$ and computes $K_{AB}=B^a(\mathrm{mod}p)$.
5. Bob’s Actions:
   • Receives ${\text{Cert}}_A$.
   • Uses $k_{pub,CA}$ to verify the signature on ${\text{Cert}}_A$.
   • If valid, he trusts that the public key $A$ inside the certificate really belongs to $I{D}_A$.
   • He extracts $A$ and computes $K_{AB}=A^b(\mathrm{mod}p)$.

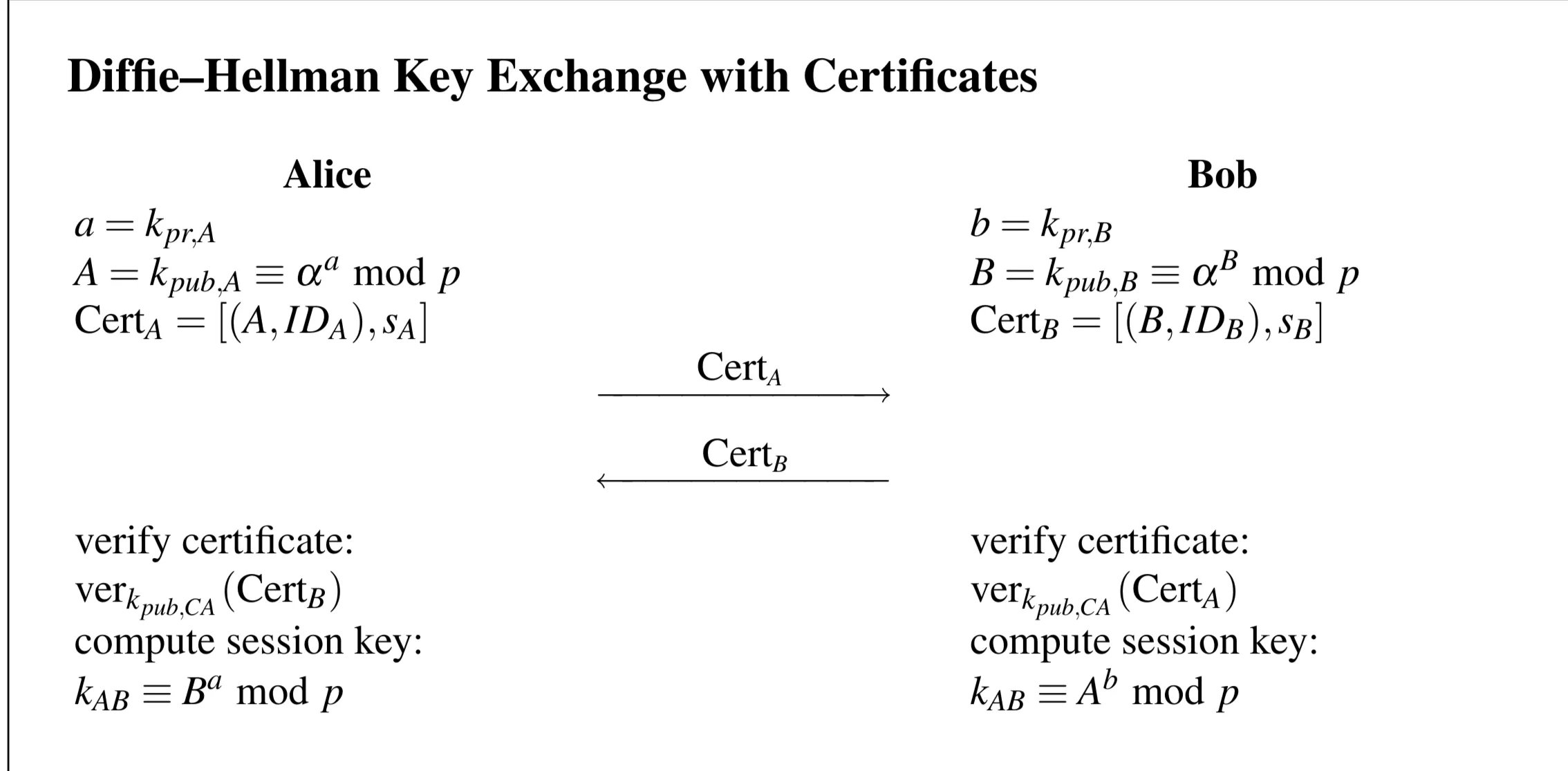
Shows DHKE with Certificates:

• Alice has $a$, computes $A$, has ${\text{Cert}}_A=[(A,I{D}_A),S_A]$ (where $S_A$ is CA’s signature).
• Bob has $b$, computes $B$, has ${\text{Cert}}_B=[(B,I{D}_B),S_B]$.
• They exchange ${\text{Cert}}_A$ and ${\text{Cert}}_B$.
• Alice verifies ${\text{Cert}}_B$ using $k_{pub,CA}$. If ok, computes $K_{AB}=B^a$.
• Bob verifies ${\text{Cert}}_A$ using $k_{pub,CA}$. If ok, computes $K_{AB}=A^b$.

MIM ATTACK FAILED

MIM Attack Failed: If Oscar tries the MIM attack now:

• He intercepts ${\text{Cert}}_A$. He can’t replace $A$ inside with his own $O$ because that would invalidate the CA’s signature $S_A$.
• He could try to get his own certificate ${\text{Cert}}_O$ from the CA for his key $O$. But this certificate would contain his identity $I{D}_O$. When Alice or Bob verify it, they would see it’s from Oscar, not from the person they intended to talk to. (Unless Oscar can fool the CA into issuing a certificate with Alice’s ID but Oscar’s key, which is a different attack on the CA’s identity verification process).

Transfer of Trust: Alice and Bob don’t need to trust each other’s keys directly. They only need to trust the CA’s public key. By verifying the CA’s signature, they transfer their trust from the CA to the public key contained in the certificate.

Public-Key Infrastructure (PKI) and The Real World

The whole system of CAs, certificates, policies, procedures for issuing and revoking certificates, etc., is called a Public-Key Infrastructure (PKI).

Real-World Complexities:

• Certificate Generation: Who generates the public/private key pair?
  • User-Provided: Alice generates her own $k_{pr,A},k_{pub,A}$ and submits $k_{pub,A}$ to the CA for signing. Requires an authenticated channel for the request. (Fig 13.14 top)
  • CA-Generated: Alice requests a certificate. The CA generates $k_{pr,A},k_{pub,A}$ for her, creates the certificate, and sends both the certificate and the private key $k_{pr,A}$ back to Alice. Requires a secure and authenticated channel for the response (since the private key is sent). (Fig 13.14 bottom)

X.509

• X.509 Certificates: A standard format for certificates used widely (e.g., in web browsers for HTTPS/SSL/TLS). Shows typical X.509 fields:
• Serial Number: Unique ID for the certificate.
• Certificate Algorithm: Which signature algorithm the CA used (e.g., RSA with SHA-256).
• Issuer: Which CA issued this certificate.
• Period of Validity: “Not Before” and “Not After” dates. Keys/certificates expire!
• Subject: The identity ($ID$) of the key owner (person, server name, etc.).
• Subject's Public Key: The actual public key and its algorithm (e.g., RSA, ECC) and parameters.
• Signature: The CA’s digital signature covering all the above fields.

• Multiple CAs & Chains of Trust: What if Alice trusts CA1, but Bob has a certificate from CA2? Alice can’t verify Bob’s certificate directly.
  • Solution: Cross-Certification. CA1 issues a certificate for CA2’s public key.
  • Chain of Trust: Alice gets ${\text{Cert}}_B$ (signed by CA2). She also gets ${\text{Cert}}_{CA2}$ (CA2’s public key, signed by CA1).
  • Alice verifies ${\text{Cert}}_{CA2}$ using CA1’s public key (which she trusts). If valid, she now trusts CA2’s public key.
  • She then uses CA2’s public key to verify ${\text{Cert}}_B$. If valid, she now trusts Bob’s public key.
  • This can form chains: Root CA certifies intermediate CAs, which certify user certificates. Your browser comes pre-loaded with the public keys of many trusted Root CAs. Illustrates this:
    • Alice has $k_{pub,CA1}$. Bob has $k_{pub,CA2}$ and ${\text{Cert}}_B$ (signed by CA2).
    • Bob sends ${\text{Cert}}_B$ to Alice. Alice can’t verify it.
    • Alice requests/receives a certificate for CA2, signed by CA1: ${\text{Cert}}_{CA2}=[(k_{pub,CA2},I{D}_{CA2}),{\text{sig}}_{k_{pr,CA1}}(...)]$
    • Alice verifies ${\text{Cert}}_{CA2}$ using $k_{pub,CA1}$. Now she trusts $k_{pub,CA2}$.
    • Alice uses $k_{pub,CA2}$ to verify ${\text{Cert}}_B$. Now she trusts $k_{pub,B}$.